Introduction

Time, which attenuates all memories, sharpens that of the Zahir.

— Jorge Luis Borges, El Zahir

Austral is a new programming language. It is designed to enable writing code that is secure, readable, maintainble, robust, and long-lasting.

Design Goals

This section lists the design goals for Austral.

1. Simplicity. This is the sine qua non: the language must be simple enough to fit in a single person’s head. We call this “fits-in-head simplicity”. Notably, many languages fail to clear this bar. C++ is the prototypical example, already its author has warned against excess complexity (in vain).

   Simplicity is valuable for multiple reasons:

   1. It makes the language easier to implement, which makes it feasible to have multiple implementations, reducing vendor lock-in risk.

   2. It makes the language easier to learn, which is good for beginners.

   3. It makes code easier to reason about, because there are fewer overlapping language features to consider.

   Simplicity is defined in terms of Kolmogorov complexity: a system is simple not when it forgives mistakes or is beginner-friendly or is easy to use. A system is simple when it can be described briefly.

   Two crucial measures of simplicity are:

   1. Language lawyering should be impossible. If people can argue about what some code prints out, that’s a language failure. If code can be ambiguous or obsfuscated, that is not a failure of the programmer but a failure of the language.

   2. A programmer should be able to learn the language in its entirety by reading this specification.

   Simplicity also means that Austral is a generally low-level language. There is no garbage collector, not primarily because of performance concerns, but because it would require an arbitrarily complex runtime.

2. Correctness. This is an intangible, but generally, the measure of how much a language enables programmers to write correct code is: if the code compiles, it should work. With the caveat that said code should use the relevant safety features, since it is possible to write unsafe C in any language.

   There is a steep tradeoff curve between correctness and simplicity: simple type system features provide 80% of correctness. The remaining 20% consists of things like:

   1. Statically proving that there are no integer overflows.
   2. Proving that all array indexing calls are within array bounds.
   3. More generally: proving that function contracts are upheld.

   Doing this with full generality requires either interactive theorem proving or SMT solving, which is a massive increase in implementational complexity (Z3 is 300,000 lines of C++). Given that this is an active area of research in computer science, we sacrifice absolute safety for implementational simplicity.

3. Security. It should not be difficult to write secure code. That is: ordinary language features should not be strewn with footguns that make security impossible.

4. Readability. We are not typists, we are programmers. And because code is read far more than it is written, we should optimize for readability, perhaps at the cost of writability.

5. Maintainability. Leslie Lamport wrote:

   An automobile runs, a program does not. (Computers run, but I’m not discussing them.) An automobile requires mainte- nance, a program does not. A program does not need to have its stack cleaned every 10,000 miles. Its if statements do not wear out through use. (Previously undetected errors may need to be corrected, or it might be necessary to write a new but sim- ilar program, but those are different matters.) An automobile is a piece of machinery, a program is some kind of mathematical expression.

   Working programmers know this is far from reality. Bitrot, not permanence, is the norm. However, bitrot is avoidable by doing careful design up-front, prioritizing stability in the design, and, crucially: saying no to proposed language features. The goal is that code written in Austral that depends only on the standard library should compile and run without changes decades into the future.

6. Modularity. Software is built out of hierarchically organized modules, accessible through interfaces. Languages have more-or-less explicit support for this:

   1. In C, all declarations exist in the same namespace, and textual inclusion and the separation of header and implementation files provides a loose modularity, enforced only through style guides and programmer discipline.

   2. In Python, modules exist, their names and paths are tied to the filesystem, and the accessibility of identifiers is determined by their names.

   3. In Rust and Java, visibility modifiers are attached to declarations to make them public or private.

   Austral’s module system is inspired by those of Ada, Modula-2, and Standard ML, with the restriction that there are no generic modules (as in Ada or Modula-3) or functors (as in Standard ML or OCaml), that is: all modules are first-order.

   Modules are given explicit names and are not tied to any particular file system structure. Modules are split in two textual parts (effectively two files), a module interface and a module body, with strict separation between the two. The declarations in the module interface file are accessible from without, and the declarations in the module body file are private.

   Crucially, a module A that depends on a module B can be typechecked when the compiler only has access to the interface file of module B. That is: modules can be typechecked against each other before being implemented. This allows system interfaces to be designed up-front, and implemented in parallel.

7. Strictness. Gerald Jay Sussman and Hal Abelson wrote:

   Pascal is for building pyramids — imposing, breathtaking, static structures built by armies pushing heavy blocks into place. Lisp is for building organisms — imposing, breathtaking, dynamic structures built by squads fitting fluctuating myriads of simpler organisms into place.

   Austral is decidedly a language for building pyramids. Code written in Austral is strict, rigid, crystalline, and brittle: minor changes are prone to breaking the build. We posit that this is a good thing.

8. Restraint. There is a widespread view in software engineering that errors are the responsibility of programmers, that “only a bad craftsperson complains about their tools”, and that the solution to catastrophic security vulnerabilities caused by the same underlying mechanisms is to simply write fewer bugs.

   We take the view that human error is an inescapable, intrinsic aspect of human activity. Human processes such as code review are only as good as the discipline of the people running them, who are often tired, burnt out, distracted, or otherwise unable to accurately simulate virtual machines (a task human brains were not evolved for), or facing business pressure to put expedience over correctness. Mechanical processes — such as type systems, type checking, formal verification, design by contract, static assertion checking, dynamic assertion checking — are independent of the skill of the programmer.

   Therefore: programmers need all possible mechanical aid to writing good code, up to the point where the implemention/semantic complexity exceeds the gains in correctness.

   Given the vast empirical evidence that humans are unable to predict the failure modes and security vulnerabilities in the code they write, Austral is designed to restrain programmer power and minimize footguns.

Rationale

This section explains and justifies the design of Austral.

Syntax

According to Wadler’s Law,

In any language design, the total time spent discussing a feature in this list is proportional to two raised to the power of its position.

0. Semantics
1. Syntax
2. Lexical syntax
3. Lexical syntax of comments

Therefore, I will begin by justifying the design of Austral’s syntax.

Austral’s syntax is characterized by:

1. Being statement-oriented rather than expression oriented.

2. Preference over English-language keywords over non-alphanumeric symbols, e.g. begin and end rather than { and }, bind over >>=, etc.

3. Delimiters include the name of the construct they terminate, e.g. end if and end for.

4. Verbose names are preferred over inscrutable abbreviations.

5. Statements are terminated by semicolons.

These decisions will be justified individually.

Statement Orientation

Syntax can be classified into three categories.

1. Statement-Oriented: Like C, Pascal, and Ada. Statements and expressions form two distinct syntactic categories.

2. Pure Expression-Oriented Syntax: Like Lisp, Standard ML, OCaml, and Haskell. There are only expressions, and the syntax reflects this directly.

3. Mixed Syntax: Many newer languages, like Scala and Rust, fall into this category. At the AST level there is only one kind of thing: expressions. But the actual written syntax is made to resemble statement-oriented languages to make programmers more comfortable.

In Epigrams in Programming, Alan Perlis wrote:

6. Symmetry is a complexity-reducing concept (co-routines include subroutines); seek it everywhere.

Indeed, expression-oriented syntax is simpler (there is no duplication between e.g. if statements and if expressions) and symmetrical (there is only one syntactic category of code). But it suffers from excess generality in that it is possible to write things like:

let x = (* A gigantic, inscrutable expression
           with multiple levels of `let` blocks. *)
in
    ...

In short, nothing forces the programmer to factor things out.

Furthermore, in pure expression-oriented languages of the ML family code has the ugly appearance of “hanging in the air”, there is little in terms of delimiters.

Three kinds of syntax.

Mixed syntaxes are unprincipled because the textual syntax doesn’t match the AST, which makes it possible to abuse the syntax and write “interesting” code. For example, in Rust, the following:

let x = { let y; }

is a valid expression. x has the Unit type because the block expression ends in a semicolon, so it is evaluated to the Unit type.

A statement-oriented syntax is less simple, but it forces code to be structurally simple, especially when combined with the restriction that uninitialized variables are not allowed. Then, the programmer is forced to factor out complicated control flow into chains of functions.

Historically, there is one language that moved from an expression-oriented to a statement-oriented syntax: ALGOL W was expression-oriented; Pascal, its successor, was statement-oriented.

Keywords over Symbols

Austral syntax prefers English-language words in place of symbols. This is because words are easier to search for, both locally and on a search engine, than a string of symbols.

Additionally, words are read into sounds, which aids in remembering them, while a string like >>= can only be understood as a visual symbol.

Using English-language keywords, however, does not mean we use a natural language inspired syntax, like Inform7. The problem with programming languages that use an English-like natural language syntax is that the syntax is a facade: programming languages are formal languages, sentences in a programming language have a rigid and ideally unambiguous interpretation.

Programming languages should not hide their formal nature under a “friendly” facade of natural language syntax.

Terminating Keywords

In Austral, delimiters include the name of the construct they terminate. This is after Ada (and the Wirth tradition) and is in contrast to the C tradition. The reason for this is that it makes it easier to find one’s place in the code.

Consider the following code:

void f() {
    for (int i = 0; i < N; i++) {
        if (test()) {
            for (int j = 0; j < N; j++) {
                if (test()) {
                    g();
                }
            }
        }
    }
}

Suppose we want to add some code after the second for loop. In this case, it’s simple enough:

void f() {
    for (int i = 0; i < N; i++) {
        if (test()) {
            for (int j = 0; j < N; j++) {
                if (test()) {
                    g();
                }
            }
            // New code goes here.
        }
    }
}

But suppose that instead of a call to g() we have multiple pages of code:

void f() {
    for (int i = 0; i < N; i++) {
        if (test()) {
            for (int j = 0; j < N; j++) {
                if (test()) {
                    // Hundreds and hundreds of lines here.
                }
            }
        }
    }
}

Then, when we scroll to the bottom of the function to add the code, we find this train of closing delimiters:

                }
            }
        }
    }
}

Which one of these corresponds to the second for loop? Unless we have an editor with folding support, we have to find the column where the second for loop begins, scroll down to the closing curly brace at that column position, and insert the code there. This is manual and error-prone.

Consider the equivalent in an Ada-like syntax:

function f() is
    for (int i = 0; i < N; i++) do
        if (test()) then
            for( int j = 0; j < N; j++) do
                if (test()) then
                    g();
                end if;
            end for;
        end if;
    end for;
end f;

Then, even if the code spans multiple pages, finding the second for loop is easy:

                end if;
            end for;
        end if;
    end for;
end f;

We have, from top to bottom:

1. The end of the second if statement.
2. The end of the second for loop.
3. The end of the first if statement.
4. The end of the first for loop.
5. The end of the function f.

Thus, delimiters which include the name of the construct they terminate involve more typing, but make code more readable.

Note that this is often done in C and HTML code, where one finds things like this:

} // access check

or,

</table> // user data table

However, declarations end with a simple end, not including the name of the declaration construct. This is because declarations are rarely nested, and including the name of the declaration would be unnecessarily verbose.

Terseness versus Verbosity

The rule is: verbose enough to be readable without context, terse enough that people will not be discouraged from factoring code into many small functions and types.

Semicolons

It is a common misconception that semicolons are needed for the compiler to know where a statement or expression ends. That is: that without semicolons, languages would be ambiguous. This obviously depends on the language grammar, but in the case of Austral it is not true, and the grammar would remain unambiguous even without semicolons.

The purpose of the semicolon is to provide redundancy, which aids both reading and parser error recovery. For example, in the following code:

let x : T := f(a, b, c;

The programmer has forgotten the closing parenthesis in a function call. However, the parser can report the error as soon as it encounters the semicolon.

For many people, semicolons represent the distinction between an old and crusty language and a modern one, in which case the semicolon serves a function similar to the use of Comic Sans by the OpenBSD project.

Syntax of Type Declarations

The syntax of type declarations it designed to make explicit the analogy between functions and generic types: that is, generic types are essentially functions from types to a new type.

Where function declarations look like this:

\[ \text{function} ~ \text{f} ( \text{p}_1: \tau_1, \dots, \text{p}_1: \tau_1 ): \tau_r ; \]

A type declaration looks like:

\[ \text{type} ~ \tau [ \text{p}_1: k, \dots, \text{p}_1: k ]: u ; \]

Here, type parameters are analogous to value parameters, kinds are analogous to types, and the universe is analogous to the return type.

Linear Types

Resource-aware type systems can remove large categories of errors that have caused endless security vulnerabilities in a simple way. This section describes the options.

This section begins with the motivation for linear types, then explains what linear types are and how they provide safety.

Resources and Lifecycles

Consider a file handling API:

type File

File openFile(String path)

File writeString(File file, String content)

void closeFile(File file)

An experienced programmer understands the implicit lifecycle of the File object:

1. We create a File handle by calling openFile.
2. We write to the handle zero or more times.
3. We close the file handle by calling closeFile.

We can depict this graphically like this:

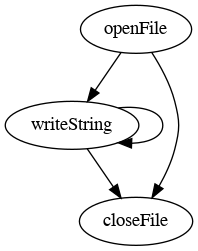
But, crucially: this lifecycle is not enforced by the compiler. There are a number of erroneous transitions that we don’t consider, but which are technically possible:

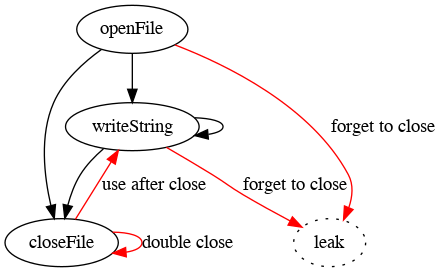
These fall into two categories:

1. Leaks: we can forget to call closeFile, e.g.:

   let file = openFile("hello.txt")
   writeString(file, "Hello, world!")
   // Forgot to close

2. Use-After-Close: and we can call writeString on a File object that has already been closed:

   closeFile(file)
   writeString(file, "Goodbye, world!");

   And we can close the file handle after it has been closed:

   closeFile(file);
   closeFile(file);

In a short linear program like this, we aren’t likely to make these mistakes. But when handles are stored in data structures and shuffled around, and the lifecycle calls are separated across time and space, these errors become more common.

And they don’t just apply to files. Consider a database access API:

type Db

Db connect(String host)

Rows query(Db db, String query)

void close(Db db)

Again: after calling close we can still call query and close. And we can also forget to call close at all.

And — crucially — consider this memory management API:

type Pointer<T>

Pointer<T> allocate(T value)

T load(Pointer<T> ptr)

void store(Pointer<T> ptr, T value)

void free(Pointer<T> ptr)

Here, again, we can forget to call free after allocating a pointer, we can call free twice on the same pointer, and, more disastrously, we can call load and store on a pointer that has been freed.

Everywhere we have resources — types with an associated lifecycle, where they must be created, used, and destroyed, in that order — we have the same kind of errors: forgetting to destroy a value, or using a value after it has been destroyed.

In the context of memory management, pointer lifecycle errors are so disastrous they have their own names:

1. Double free errors.
2. Use-after-free errors.

Naturally, computer scientists have attempted to attack these problems. The traditional approach is called static analysis: a group of PhD’s will write a program that goes through the source code and performs various checks and finds places where these errors may occur.

Reams and reams of papers, conference proceedings, university slides, etc. have been written on the use of static analysis to catch these errors. But the problem with static analysis is threefold:

1. It is a moving target. While type systems are relatively fixed — i.e., the type checking rules are the same across language versions — static analyzers tend to change with each version, so that in each newer version of the software you get more and more sophisticated heuristics.

2. Like unit tests, it can usually show the presence of bugs, but not their absence. There may be false positives — code that is perfectly fine but that the static analyzer flags as incorrect — but more dangerous is the false negative, where the static analyzer returns an all clear on code that has a vulnerability.

3. Static analysis is an opaque pile of heuristics. Because the analyses are always changing, the programmer is not expected to develop a mental model of the static analyzer, and to write code with that model in mind. Instead, they are expected to write the code they usually write, then throw the static analyzer at it and hope for the best.

What we want is a way to solve these problems that is static and complete. Static in that it is a fixed set of rules that you can learn once and remember, like how a type system works. Complete in that is has no false negatives, and every lifecycle error is caught.

And, above all: we want it to be simple, so it can be wholly understood by the programmer working on it.

So, to summarize our requirements:

1. Correctness Requirement: We want a way to ensure that resources are used in the correct lifecycle.

2. Simplicity Requirement: We want that mechanism to be simple, that is, a programmer should be able to hold it in their head. This rules out complicated solutions involving theorem proving, SMT solvers, symbolic execution, etc.

3. Staticity Requirement: We want it to be a fixed set of rules and not an ever changing pile of heuristics.

All these goals are achievable: the solution is linear types.

Linear Types

This section describes what linear types are, how they provide the safety properties we want, and how we can relax some of the more onerous restrictions so as to increase programmer ergonomics while retaining safety.

A type is a set of values that share some structure. A linear type is a type whose values can only be used once. This restriction may sound onerous (and unrelated to the problems we want to solve), but it isn’t.

A linear type system can be defined with just two rules:

1. Linear Universe Rule: in a linear type system, the set of types is divided into two universes: the free universe, containing types which can be used any number of times (like booleans, machine sized integers, floats, structs containing free types, etc.); and the linear universe, containing linear types, which usually represent resources (pointers, file handles, database handles, etc.).

   Types enter the linear universe in one of two ways:

   1. By fiat: a type can simply be declared linear, even though it only contains free types. We’ll see later why this is useful.

      // `LInt` is in the `Linear` universe,
      // even if `Int` is in the `Free` universe.
      type LInt: Linear = Int

   2. By containment: linear types can be thought of as being “viral”. If a type contains a value of a linear type, it automatically becomes linear.

      So, if you have a linear type T, then a tuple (a, b, T) is linear, a struct like:

      struct Ex {
          a: A;
          b: B;
          c: Pair<T, A>;
      }

      is linear because the slot c contains a type which in turn contains T. A union or enum where one of the variants contains a linear type is, unsurprisingly, linear. You can’t sneak a linear type into a free type.

   The virality of linear types ensures that you can’t escape linearity by accident.

2. Use-Once Rule: a value of a linear type must be used once and only once. Not can: must. It cannot be used zero times. This can be enforced entirely at compile time through a very simple set of checks.

   To understand what “using” a linear value means, let’s look at some examples. Suppose you have a function f that returns a value of a linear type L.

   Then, the following code:

   {
       let x: L := f();
   }

   is incorrect. x is a variable of a linear type, and it is used zero times. The compiler will complain that x is being silently discarded.

   Similarly, if you have:

   {
       f();
   }

   The compiler will complain that the return value of f is being silently discarded, which you can’t do to a linear type.

   If you have:

   {
       let x: L := f();
       g(x);
       h(x);
   }

   The compiler will complain that x is being used twice: it is passed into g, at which point is it said to be consumed, but then it is passed into h, and that’s not allowed.

   This code, however, passes: x is used once and exactly once:

   {
       let x: L := f();
       g(x);
   }

   “Used” does not, however, mean “appears once in the code”. Consider how if statements work. The compiler will complain about the following code, because even though x appears only once in the source code, it is not being “used once”, rather it’s being used — how shall I put it? 0.5 times?:

   {
       let x: L := f();
       if (cond) {
           g(x);
       } else {
           // Do nothing.
       }
   }

   x is consumed in one branch but not the other, and the compiler isn’t happy. If we change the code to this:

   {
       let x: L := f();
       if (cond) {
           g(x);
       } else {
           h(x);
       }
   }

   Then we’re good. The rule here is that a variable of a linear type, defined outside an if statement, must be used either zero times in that statement, or exactly once in each branch.

   A similar restriction applies to loops. We can’t do this:

   {
       let x: L := f();
       while (true) {
           g(x);
       }
   }

   Because even though x appears once, it is used more than once: it is used once in each iteration. The rule here is that a variable of a linear type, defined outside a loop, cannot appear in the body of the loop.

That’s it. That’s all there is to it. We have a fixed set of rules, and they’re so brief you can learn them in a few minutes. So we’re satisfying the simplicity and staticity requirements listed in the previous section.

But do linear types satisfy the correctness requirement? In the next section, we’ll see how linear types make it possible to enforce that a value should be used in accordance to a lifecycle.

Linear Types and Safety

Let’s consider a linear file system API. We’ll use a vaguely C++ like syntax, but linear types are denoted by an exclamation mark after their name.

The API looks like this:

type File!

File! openFile(String path)

File! writeString(File! file, String content)

void closeFile(File! file)

The openFile function is fairly normal: takes a path and returns a linear File! object.

writeString is where things are different: it takes a linear File! object (and consumes it), and a string, and it returns a “new” linear File! object. “New” is in quotes because it is a fresh linear value only from the perspective of the type system: it is still a handle to the same file. But don’t think about the implementation too much: we’ll look into how this is implemented later.

closeFile is the destructor for the File! type, and is the terminus of the lifecycle graph: a File! enters and does not leave, and the object is disposed of. Let’s see how linear types help us write safe code.

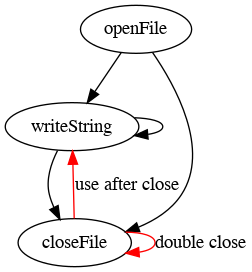
Can we leak a File! object? No:

let file: File! := openFile("sonnets.txt");
// Do nothing.

The compiler will complain: the variable file is used zero times. Alternatively:

let file: File! := openFile("sonnets.txt");
writeString(file, "Devouring Time, blunt thou the lion’s paws, ...");

The return value of writeString is a linear File! object, and it is being silently discarded. The compiler will whine at us.

We can strike the “leak” transitions from the lifecycle graph:

Can we close a file twice? No:

let file: File! := openFile("test.txt");
closeFile(file);
closeFile(file);

The compiler will complain that you’re trying to use a linear variable twice. So we can strike the “double close” erroneous transition from the lifecycle graph:

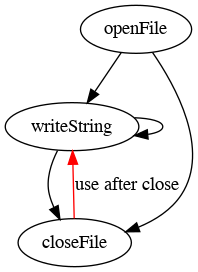
And you can see where this is going. Can we write to a file after closing it? No:

let file: File! := openFile("test.txt");
closeFile(file);
let file2: File! := writeString(file, "Doing some mischief.");

The compiler will, again, complain that we’re consuming file twice. So we can strike the “use after close” transition from the lifecycle graph:

And we have come full circle: the lifecycle that the compiler enforces is exactly, one-to-one, the lifecycle that we intended.

There is, ultimately, one and only one way to use this API such that the compiler doesn’t complain:

let f: File! := openFile("rilke.txt");
let f_1: File! := writeString(f, "We cannot know his legendary head\n");
let f_2: File! := writeString(f_1, "with eyes like ripening fruit. And yet his torso\n");
...
let f_15: File! := writeString(f_14, "You must change your life.");
closeFile(f_15);

Note how the file value is “threaded” through the code, and each linear variable is used exactly once.

And now we are three for three with the requirements we outlined in the previous section:

1. Correctness Requirement: Is it correct? Yes: linear types allow us to define APIs in such a way that the compiler enforces the lifecycle perfectly.

2. Simplicity Requirement: Is it simple? Yes: the type system rules fit in a napkin. There’s no need to use an SMT solver, or to prove theorems about the code, or do symbolic execution and explore the state space of the program. The linearity checks are simple: we go over the code and count the number of times a variable appears, taking care to handle loops and if statements correctly. And also we ensure that linear values can’t be discarded silently.

3. Staticity Requirement: Is it an ever-growing, ever-changing pile of heuristics? No: it is a fixed set of rules. Learn it once and use it forever.

And does this solution generalize? Let’s consider a linear database API:

type Db!

Db! connect(String host)

Pair<Db!, Rows> query(Db! db, String query)

void close(Db! db)

This one’s a bit more involved: the query function has to return a tuple containing both the new Db! handle, and the result set.

Again: we can’t leak a database handle:

let db: Db! := connect("localhost");
// Do nothing.

Because the compiler will point out that db is never consumed. We can’t close a database handle twice:

let db: Db! := connect("localhost");
close(db);
close(db); // error: `db` consumed again.

Because db is used twice. Analogously, we can’t query a database once it’s closed:

let db: Db! := connect("localhost");
close(db);
let (db1, rows): Pair<Db!, Rows> := query(db, "SELECT ...");
close(db); // error: `db` consumed again.

For the same reason. The only way to use the database correctly is:

let db: Db! := connect("localhost");
let (db1, rows): Pair<Db!, Rows> := query(db, "SELECT ...");
// Iterate over the rows or some such.
close(db1);

What about manual memory management? Can we make it safe? Let’s consider a linear pointer API, but first, we have to introduce some new notation. When you have a generic type with generic type parameters, in a regular language you might declare it like:

type T<A, B, C>

Here, we also have to specify which universe the parameters and the resulting type belong to. Rember: there are two universes: free and linear. So for example we can write:

type T<A: Free, B: Free>: Free
type U!<A: Linear>: Linear

But sometimes we want a generic type to accept type arguments from any universe. In that case, we use Type:

type Pair<L: Type, R: Type>: Type;

This basically means: the type parameters L and R can be filled with types from either universe, and the universe that Pair belongs to is determined by said arguments:

1. If A and B are both Free, then Pair is Free.
2. If either one of A and B are Linear, then Pair is Linear.

Now that we’re being explicit about universes, we can drop the exclamation mark notation.

Here’s the linear pointer API:

type Pointer<T: Type>: Linear;

generic <T: Type>
Pointer<T> allocate(T value)

generic <T: Type>
T deallocate(Pointer!<T> ptr)

generic <T: Free>
Pair<Pointer<T>, T> load(Pointer<T> ptr)

generic <T: Free>
Pointer<T> store(Pointer<T> ptr, T value)

This is more involved than previous examples, and uses new notation, so let’s break it down declaration by declaration.

1. First, we declare the Pointer type as a generic type that takes a parameter from any universe, and belongs to the Linear universe by fiat. That is: even if T is Free, Pointer<T> will be Linear.

   type Pointer<T: Type>: Linear;

2. Second, we define a generic function allocate, that takes a value from either universe, allocates memory for it, and returns a linear pointer to it.

   generic <T: Type>
   Pointer<T> allocate(T value)

3. Third, we define a slightly unusual deallocate function: rather than returning void, it takes a pointer, dereferences it, deallocates the memory, and returns the dereferenced value:

   generic <T: Type>
   T deallocate(Pointer!<T> ptr)

4. Fourth, we define a generic function specifically for pointers that contain free values: it takes a pointer, dereferences it, and returns a tuple with both the pointer and the dereferenced free value.

   generic <T: Free>
   (Pointer<T>, T) load(Pointer<T> ptr)

   Why does T have to belong to the Free universe? Because otherwise we could write code like this:

   // Suppose that `L` is a linear type.
   let p: Pointer<L> := allocate(...);
   let (p2, val): Pair<Pointer<L>, L> := load(p);
   let (p3, val2): Pair<Pointer<L>, L> := load(p2);

   Here, we’ve allocated a pointer to a linear value, but we’ve loaded it from memory twice, effectively duplicating it. This obviously should not be allowed. So the type parameter T is constrained to take only values of the Free universe, which can be copied freely any number of times.

5. Fifth, we define a generic function, again for pointers that contain free values. It takes a pointer and a free value, and stores that value in the memory allocated by the pointer, and returns the pointer again for reuse:

   generic <T: Free>
   Pointer<T> store(Pointer<T> ptr, T value)

   Again: why can’t this function be defined for linear values? Because then we could write:

   // Suppose `L` is a linear type, and `a` and b`
   // are variables of type `L`.
   let p1: Pointer<L> := allocate(a);
   let p2: Pointer<L> := store(p1, b);
   let l: L := deallocate(p2);

   What happens to a? It is overwritten by b and lost. For values in the Free universe this is no problem: who cares if a byte is overwritten? But we can’t overwrite linear values – like database handles and such – because the they would be leaked.

It is trivial to verify the safety properties. We can’t leak memory, we can’t deallocate twice, and we can’t read or write from and to a pointer after it has been deallocated.

What Linear Types Provide

Linear types give us the following benefits:

1. Manual memory management without memory leaks, use-after-free, double free errors, garbage collection, or any runtime overhead in either time or space other than having an allocator available.

2. More generally, we can manage any resource (file handles, socket handles, etc.) that has a lifecycle in a way that prevents:

   1. Forgetting to dispose of that resource (e.g.: leaving a file handle open).
   2. Disposing of the resource twice (e.g.: trying to free a pointer twice).
   3. Using that resource after it has been disposed of (e.g.: reading from a closed socket).

   All of these errors are prevented statically, again without runtime overhead.

3. In-place optimization: the APIs we have looked at resemble functional code. We write code “as if” we were creating and returning new objects with each call, while doing extensive mutations under the hood. This gives us the benefits of functional programming (referential transparency and equational reasoning) with the performance of imperative code that mutates data wildly.

4. Safe concurrency. A value of a linear type, by definition, has only one owner: we cannot duplicate it, therefore, we cannot have multiple owners across threads. So imperative mutation is safe, since we know that no other thread can write to our linear value while we work with it.

5. Capability-based security: suppose we want to lock down access to the terminal. We want there to be only one thread that can write to the terminal at a time. Furthermore, code that wants to write to the terminal needs permission to do so.

   We can do this with linear types, by having a linear Terminal type that represents the capability of using the terminal. Functions that read and write from and to the terminal need to take a Terminal instance and return it. We’ll discuss capability based security in greater detail in a future section.

The Trust Boundary

So far we have only seen the interfaces of linear APIs. What about the implementations?

Here’s the linear file access API, using the universe notation instead of the exclamation mark notation to indicate linear types:

type File: Linear

File openFile(String path)

File writeString(File file, String content)

void closeFile(File file)

How does writeString respect linearity? Clearly, it is consuming a File handle, then returning it again. Does it internally close and reopen the file handle?

The answer involves the concept of a trust boundary: inside the File type is a plain old fashioned (unrestricted, non-linear) file handle, like so:

struct File: Linear {
  handle: int;
}

The openFile function looks like this:

extern int fopen(char* filename, char* mode)

File openFile(String path) {
    let ptr: int = fopen(as_c_string(filename), "r");
    return File(handle => ptr);
}

openFile calls fopen, which returns a file handle as an ordinary, free integer. Then we wrap it in a nice linear type and return it to the client.

Write string is where the magic happens:

extern int fputs(char* string, int fp)

File writeString(File file, String content) {
  let { handle: int } := file;
  fputs(as_c_string(content), handle);
  return File(handle => handle);
}

The let statement uses destructuring syntax: it “explodes” a linear struct into a set of variables.

Why do we need destructuring? Imagine if we had a struct with two linear fields:

struct Pair {
  x: L1;
  y: L2;
}

And we wanted to write code like:

let p: Pair := make_pair();
let x: L1 := p.x;

This is a big problem. p is being consumed by the p.x expression. But what happens to the y field in the p struct? It is leaked: we can’t afterwards write p.y because p has been consumed.

Austral has special rules around accessing the fields of a struct to prevent this kind of situation. And the destructuring syntax we’re using allows us to take a struct, dismantle it into its constituent fields (linear or otherwise), then transform the values of those fields and/or put them back together.

This is what we’re doing in openFile: we break up the File value into its constituent fields (here just handle), which consumes it. Then we call fputs on the non-linear handle, then, we construct a new instance of File that contains the unchanged file handle.

From the compiler’s perspective, the File that goes in is distinct from the File that goes out and linearity is respected. Internally, the non-linear handle is the same.

Finally, closeFile looks like this:

extern int fclose(int fp)

void closeFile(File file) {
  let { handle: int } := file;
  fclose(handle);
}

The file variable is consumed by being destructured. Then we call fclose on the underlying file handle.

And there you have it: linear interface, non-linear interior. Inside the trust boundary, there is a light amount of unsafe FFI code (ideally, carefully vetted and tested). Outside, there is a linear interface, which can only be used correctly.

Affine Types

Affine types are a “weakening” of linear types. Where linear types are “use exactly once”, affine types are “use at most once”. Values can be silently discarded.

This requires a way to associate destructors to affine types. Then, at the end of a block, the compiler will look around for unconsumed affine values, and insert calls to their destructors.

There are two benefits to affine types:

1. First, by using implicit destructors, the code is less verbose.

2. Secondly (and this will be expanded upon in the next section), affine types are compatible with traditional (C++ or Java-style) exception handling, while linear types are not.

But there are downsides:

1. Sometimes, you don’t want values to be silently discarded.

2. There are implicit function calls (destructor calls are inserted by the compiler at the end of blocks).

3. Exception handling involves a great deal of complexity, and is not immune to e.g. the “double throw” problem.

Borrowing

Returning tuples from every function and threading linear values through the code is very verbose.

It is also often a violation of the principle of least privilege: linear values, in a sense, have “uniform permissions”. If you have a linear value, you can destroy it. Consider the linear pointer API described above: the load function could internally deallocate the pointer and allocate it again.

We wouldn’t expect that to happen, but the whole point is to be defensive. We want the language to give us some guarantees: if a function should only be allowed to read from a linear value, but not deallocate it or mutate its interior, we want a way to represent that.

Borrowing is stolen lock, stock, and barrel from Rust. It advanced programming ergonomics by allowing us to treat a linear value as free within a delineated context. And it allows us to degrade permissions: we can pass read-only references to a linear value to functions that should only be able to read from that value, we can pass mutable references to a linear value to functions that should only be able to read from, and mutate, that value, without destroying it. Passing the linear value itself is the highest level of permissions: it allows the receiving function to do anything whatever with that value, by taking complete ownership of it.

The Cutting Room Floor

Universes are not the only way to implement linear types. There are three ways:

1. Linearity via arrows, as in the linear types extension of the GHC compiler for Haskell. This is the closest to Girard’s linear logic.

2. Linearity via kinds, which involves partitioning the set of types into two universes: a universe of unrestricted values which can be copied freely, such as integers, and a universe of restricted or linear types.

3. Rust’s approach, which is a sophisticated, fine-grained ownership tracking scheme.

In my opinion, linearity via arrows is best suited to an ML family language with single-parameter functions.

Rust’s ownership tracking scheme allows programmers to write code that looks quite ordinary, frequently using values multiple times, while retaining “linear-like” properties. Ordinarily the restrictions show up when compilation fails.

The Rust approach prioritizes programmer ergonomics, but it has a downside: the ownership tracking scheme is not a fixed algorithm that is set in stone in a standards document, which programmers are expected to read in order to write code. Rather, it is closer to static analysis in that it is a collection of rules, which evolve with the language, generally in the direction of improving ergonomics and allowing programmers to focus on the problem at hand rather than bending the code to fit the ownership scheme. Consequently, Rust programmers often describe a learning curve with a period of “fighting the borrow checker”, until they become used to the rules.

Compare this with type checking algorithms: type checking is a simple, inductive process, so much so that programmers effectively run the algorithm while reading code to understand how it behaves. It often does not need documenting because it is obvious whether or not two types are equal or compatible, and the “warts” are generally in the area of implicit integer or float type conversions in arithmetic, and subtyping where present.

There are many good reasons to prefer the Rust approach:

1. Programmers care a great deal about ergonomics. The dangling else is a feature of C syntax that has caused many security vulnerabilities. Try taking this away from programmers: they will kick and scream about the six bytes they’re saving on each if statement.

2. Allowing programmers to write code that they’re used to helps with onboarding new users. It is generally not realistic to tell programmers to “read the spec” to learn a new language.

3. By putting the complexity in the language, application code becomes simpler: programmers can focus on solving the problem at hand, and the compiler, ever helpful, will do its best to “prove around it”, that is, the compiler bends to the programmer’s code and tries to interpret it as best it can, rather than the programmer bending to the language’s rules.

4. Since destructors are automatically inserted, the code is less verbose.

5. Finally, Rust’s approach is compatible with exception handling, which the language provides: panics unwind the stack and call destructors automatically. Austral, because of its emphasis on implementation simplicty, has much more verbose code around error handling.

Austral takes the approach that a language should be simple enough that it can be understood entirely by a single person reading the specification. Consequently, a programmer should be able to read a brief set of linearity checker rules, and afterwards be able to write code without fighting the system, or failing to understand how or why some code compiles.

In short: we sacrifice terseness and programmer ergonomics for simplicity. Simple to learn, simple to understand, simple to reason about.

To do this, we choose linearity via kinds, because it provides the simplest way to implement a linear type system. The set of unrestricted types is called the “free universe” and is denoted Free (because Unrestricted takes too much typing) and the set of restricted or linear types is called the “linear universe” and is denoted Linear.

Another feature that was considered and discarded is LinearML’s concept of observer types, a lightweight alternative to read-only references that has the benefit of not requiring regions, but has the drawback that they can’t be stored in data structures.

Conclusion

In the next section, we explain the rationale for Austral’s approach to error handling, why linear types are incompatible with traditional exception handling, what affine types are, and how our preferred error handling scheme impacts the choice of linear types over affine types.

Afterwards, we describe capability-based security, and how linear types allow us to implement capabilities.

Error Handling

On July 3, 1940, as part of Operation Catapult, Royal Air Force pilots bombed the ships of the French Navy stationed off Mers-el-Kébir to prevent them falling into the hands of the Third Reich.

This is Austral’s approach to error handling: scuttle the ship without delay.

In software terms: programs should crash at the slightest contract violation, because recovery efforts can become attack vectors. You must assume, when the program enters an invalid state, that there is an adversary in the system. For failures — as opposed to errors — you should use Option and Result types.

This section describes the rationale for Austral’s approach to error handling. We begin by describing what an error is, then we survey different error handling strategies. Then we explain how those strategies impinge upon a linear type system.

Categorizing Errors

“Error” is a broad term. Following Sutter and the Midori error model, we divide errors into the following categories:

1. Physical Failure: Pulling the power cord, destroying part of the hardware.

2. Abstract Machine Corruption: A stack overflow.

3. Contract Violations: Due to a mistake the code, the program enters an invalid state. This includes:

   1. An arithmetic operation leads to integer overflow or underflow (the contract here is that operands should be such that the operation does not overflow).

   2. Integer division by zero (the contract is the divisor should be non zero).

   3. Attempting to access an array with an index outside the array’s bounds (the contract is that the index should be within the length of the array).

   4. Any violation of a programmer-defined precondition, postcondition, assertion or invariant.

   These errors are bugs in the program. They are unpredictable, often happen very rarely, and can open the door to security vulnerabilities.

4. Memory Allocation Failure: malloc returns null, essentially. This gets its own category because allocation is pervasive, especially in higher-level code, and allocation failure is rarely modeled at the type level.

5. Failure Conditions. “File not found”, “connection failed”, “directory is not empty”, “timeout exceeded”.

We can pare down what we have to care about:

1. Physical Failure: Nothing can be done. Although it is possible to write software that persists data in a way that survives e.g. power failure. Databases are often implemented in this way.

2. Abstract Machine Corruption. The program should terminate. At this point the program is in a highly problematic state and any attempt at recovery is likely counterproductive and possibly enables security vulnerabilities.

3. Memory Allocation Failure: Programs written in a functional style often rely on memory allocation at arbitrary points in the program execution. Allocation failure in a deeply nested function thus presents a problem from an error-handling perspective: if we’re using values to represent failures, then every function that allocates has to return an Optional type or equivalent, and this propagates up through every client of that function.

   Nevertheless, returning an Optional type (or equivalent) on memory allocation is sufficient. It places a minor burden on the programmer, who has to explicitly handle and propagate these failures, but this burden can be eased by refactoring the program so that most allocations happen in the same area in time and space.

   This type of refactoring can improve performance, as putting allocations together will make it clear when there is an opportunity to replace \(n\) allocations of an object of size \(k\) bytes with a single allocation of an array of \(n \times k\) bytes.

   A common misconception is that checking for allocation failure is pointless, since a program might be terminated by the OS if memory is exhausted, or because platforms that implement memory overcommit (such as Linux) will always return a pointer as though allocation had succeeded, and crash when writing to that pointer. This is a misconception for the following reasons:

   1. Memory overcommit on Linux can be turned off.

   2. Linux is not the only platform.

   3. Memory exhaustion is not the only situation where allocation might fail: if memory is sufficiently fragmented that a chunk of the requested size is not available, allocation will fail.

4. Failure Conditions. These errors are recoverable, in the sense that we want to catch them and do something about them, rather than crash. Often this involves prompting the user for corrected information, or otherwise informing the user of failure, e.g. if trying to open a file on a user-provided path, or trying to connect to a server with a user-provided host and port.

   Consequently, these conditions should be represented as values, and error handling should be done using standard control flow.

   Values that represent failure should not be confused with “error codes” in languages like C. “Error codes or exceptions” is a false dichotomy. Firstly, strongly-typed result values are better than brittle integer error codes. Secondly, an appropriate type system lets us have e.g. Optional or Result types to better represent the result of fallible computations. Thirdly, a linear type system can force the programmer to check result codes, so the argument that error codes are bad because programmers might forget to check them is obviated.

That takes care of four of five categories. There’s one left: what do we do about contract violations? How we choose to handle this is a critical question in the design of any programming language.

Error Handling for Contract Violations

There are essentially three approaches, from most to least brutal:

1. Terminate Program: When a contract violation is detected, terminate the entire program. No cleanup code is executed. Henceforth “TPOE” for “terminate program on error”.

2. Terminate Thread: When a contract violation is detected, terminate the current thread or task. No cleanup code is executed, but the parent thread will observe the failure, and can decide what to do about it. Henceforth “TTOE” for “terminate thread/task on error”.

3. Traditional Exception Handling: Raise an exception/panic/abort (pick your preferred terminology), unwind the stack while calling destructors. This is the approach offered by C++ and Rust, and it integrates with RAII. Henceforth “REOE” for “raise exception on error”.

Terminate Program

The benefit of this approach is simplicity and security: from the perspective of security vulnerabilities, terminating a program outright is the best thing to do,

If the program is the target of an attacker, cleanup or error handling code might inadvertently allow an attacker to gain access to the program. Terminating the program without executing any cleanup code at all will prevent this.

The key benefit here besides security is simplicty. There is nothing simpler than calling _exit(-1). The language is simpler and easier to understand. The language also becomes simpler to implement. The runtime is simpler. Code written in the language is simpler to understand and reason about: there are no implicit function calls, no surprise control flow, no complicated unwinding schemes.

There are, however, a number of problems:

1. Resource Leaks: Depending on the program and the operating system, doing this might leak resources.

   If the program only allocates memory and acquires file and/or socket handles, then the operating system will likely be able to garbage-collect all of this on program termination. If the program uses more exotic resources, such as locks that survive program termination, then the system as a whole might enter an unusable state where the program cannot be restarted (since the relevant objects are still locked), and human intervention is needed to delete those surviving resources.

   For example, consider a build. The program might use a linear type to represent the lifecycle of the directory that stores build output. A create function creates the directory if it does not already exist, a corresponding destroy function deletes the directory and its contents.

   If the program is terminated before the destroy function is called, running the program again will fail in the call to create because the directory already exists.

   Additionally, in embedded systems without an operating system, allocated resources that are not cleaned up by the program will not be reclaimed by anything.

2. Testing: In a testing framework, we often want to test that a function will not fail on certain inputs, or that it will definitely fail on certain others. For example, we may want to test that a function correctly aborts on values that don’t satisfy some precondition.

   JUnit, for example, provides assertThrows for this purpose.

   If contract violations terminate the program, then the only way to write an assertAborts function is to fork the process, run the function in the child process, and have the parent process observe whether or not it crashes. This is expensive. And if we don’t implement this, a contract violation will crash the entire unit testing process.

   This is a problem because, while we are implicitly “testing” for contract violations whenever a function is called, it is still good to have explicit unit tests that we can point to in order to prove that a function does indeed reject certain kinds of values.

3. Exporting Code: When exporting code through the FFI, terminating the program on contract violations is less than polite.

   If we write a library and export its functionality through the FFI so it is accessible from other languages, terminating the process from that library will crash everything else in the address space. All the code that uses our library can potentially crash on certain obscure error conditions, a situation that would be extremely difficult to debug due to its crossing language boundaries.

   The option of forking the process, in this context, is prohibitively expensive.

Terminate Thread on Error

Terminating the thread where the contract violation happened, rather than the entire process, gives us a bit more recoverability and error reporting ability, at the cost of safety and resource leaks.

The benefit is that calling a potentially-failing function safely “only” requires spawning a new thread. While expensive (and not feasible in a function that might be called thousands of times a second) this is significantly cheaper than forking the process.

A unit testing library could plausibly do this to implement assertions that a program does or does not violate any conditions. Condition failures could then be reported within the unit testing framework as just another failing test, without crashing the entire process or requiring expensive forking of the process.

If we split programs into communicating threads, the failure of one thread could be detected by its parent, and reported to the user before the program is terminated.

This is important: the program should still be terminated. Terminating the thread, rather than the entire program, is inteded to allow more user-friendly and complete reporting of failures, not as a general purpose error recovery mechanism.

For example, in the context of a webserver, we would not want to restart failed server threads. Since cleanup code is not executed on thread termination, a long running process which restarts failing threads will eventually run out of memory or file handles or other resources.

An attacker that knows the server does this could execute a denial of service attack by forcing a previously undetected contract violation.

Raise Exception on Error

This is traditional exception handling with exception values, stack unwinding, and destructors. C++ calls this throwing an exception. Rust and Go call it panicking. The only technical difference between C++ exception handling and Go/Rust panics is that C++ exceptions can be arbitrarily sized objects (and consequently throwing requires a memory allocation) while in Go and Rust panics can at most carry an error message. Ada works similarly: an exception is a type tag plus an error message string.

When a contract violation is detected, an exception is raised and stack unwinding begins. The stack unwinding process calls destructors. If an appropriate handler is reached, control transfers to that handler after stack unwinding. If no handler is reached, the thread is terminated, and the parent thread receives the exception object.

Implementing exception handling mainly requires having a way to associate types with destructors.

When a value goes out of scope or its scope is entire wiped by stack unwinding, we need to destroy that value. This is done by destructors: functions A -> Unit that consume the value, deallocate it, close file handles etc. and return nothing.

Type classes are enough to implement destructors. We’d have a typeclass:

typeclass Destructable(T) is
    method destroy(value: T): Unit;
end;

And implement instances for types that need cleanup. Then the compiler inserts destructor calls at the end of scope and in stack unwinding code.

The benefits of this approach are:

1. Resource Safety: Contract violations will unwind the stack and cause destructors to be called, which allows us to safely deallocate resources (with some caveats, see below).

   We can write servers where specific worker threads can occasionally tip over, but the file/socket handles are safely closed, and the entire server does not crash.

   When the parent thread of a failing thread receives an exception, it can decide whether to restart the thread, or simply rethrow the exception. In the latter case, its own stack would be unwound and its own resources deallocated. Transitively, an exception that is not caught anywhere and reaches the top of the stack will terminate the program only after all resources have been safely deallocated.

2. Testing: Contract violations can be caught during test execution and reported appropriately, without needing to spawn a new thread or a new process.

3. Exporting Code: Code that is built to be exported through the C ABI can catch all exceptions, convert them to values, and return appropriate error values through the FFI boundary. Rust libraries that export Rust code through the FFI use catch_unwind to do this.

There are, however, significant downsides to exception handling:

1. Complexity: Exceptions are among the most complex language features. This complexity is reflected in the semantics, which makes the language harder to describe, harder to formalize, harder to learn, and harder to implement. Consequently the code is harder to reason about, since exceptions introduce surprise control flow at literally every program point.

2. Pessimization: When exceptions are part of the language semantics, and any function can throw, many compiler optimizations become unavailable.

3. Code Size: Exception handling support, even so called “zero cost exception handling”, requires sizeable cleanup code to be written. This has a cost in the size of the resulting binaries. Larger binaries can result in a severe performance penalty if the code does not fit in the instruction cache.

4. Hidden Function Calls: Calls to destructors are inserted by the compiler, both on normal exit from a scope and on cleanup. This makes destructors an invisible cost.

   This is worsened by the fact that destructors are often recursive: destroying a record requires destroying every field, destroying an array requires destroying every element.

5. No Checking: exceptions bypass the type system. Solutions like checked exceptions in Java exist, but are unused, because they provide little benefit in exchange for onerous restrictions. The introduction of checked exceptions is also no small matter: it affects the specification of function signatures and generic functions, since you need a way to do “throwingness polymorphism” (really, effect polymorphism). Any function that takes a function as an argument has to annotate not just the function’s type signature but its permitted exception signature.

6. Pervasive Failure: If contract violations can throw, then essentially every function can throw, because every function has to perform arithmetic, either directly or transitively. So there is little point to a throws annotation like what Herb Sutter suggests or Swift provides, let alone full blown checked exceptions, since every function would have to be annotated with throws (Overflow_Error).

7. Double Throw Problem: What do we do when the destructor throws? This problem affects every language that has RAII.

   In C++ and Rust, throwing in the destructor causes the program to abort. This an unsatisfactory solution: we’re paying the semantic and runtime cost of exceptions, stack unwinding, and destructors, but a bug in the destructor invalidates all of this. If we’re throwing on a contract violation, it is because we expect the code has bugs in it and we want to recover gracefully from those bugs. Therefore, it is unreasonable to expect that destructors will be bug-free.

   Ada works differently in that raising an exception in a finalizer throws an entirely new exception (discarding the original one).

   Double throw is not necessarily a pathological edge case either: the fclose function from the C standard library returns a result code. What should the destructor of a file object do when fclose returns an error code?

   In Rust, according to the documentation of the std::fs::File object: “Files are automatically closed when they go out of scope. Errors detected on closing are ignored by the implementation of Drop. Use the method sync_all if these errors must be manually handled.”

   A solution would be to store a flag in the file object that records the state of the file handle: either closed or open. Then, we can have a function close : File -> ReturnCode that calls fclose, sets the flag to closed, and returns the return code for the client to handle. The destructor would then check that flag: if the flag is open, it calls fclose, ignoring the return code (or aborting if fclose reports an error), and if the flag is closed, the destructor does nothing.

   But this is a non-solution.

   1. With affine types and RAII, we cannot force the programmer to call the close function. If a file object is silently discarded, the compiler will insert a call to the destructor, which as we’ve seen makes fewer safety guarantees. So we have a type system to manage resources, but it doesn’t force us to handle them properly.

   2. We’re paying a cost, in space and time, in having a flag that records the file handle state and which needs to be set and checked at runtime. The whole point of resource management type systems is the flag exists at compile time. Otherwise we might as well have reference counting.

8. Compile Time: Compilers anecdotally spend a lot of time compiling landingpads.

9. Non-Determinism: Time and space cost of exceptions is completely unknown and not amenable to static analysis.

10. Platform-Specific Runtime Support: Exceptions need support from the runtime, usually involving the generation of DWARF metadata and platform specific assembly. This is the case with Itanium ABI “zero-cost exceptions” for C++, which LLVM implements.

11. Corruption: Unwinding deallocates resources, but this is not all we need. Data structures can be left in a broken, inconsistent state, the use of which would trigger further contract violations when their invariants are violated.

    This can be mitigated somewhat by not allowing the catching of exceptions except at thread boundaries, beyond which the internal broken data structures cannot be observed. Thus threads act as a kind of censor of broken data. Providing the strong exception guarantee requires either transactional memory semantics (and their implied runtime cost in both time, space, and implementation complexity) or carefully writing every data structure to handle unwinding gracefully.

    However, making it impossible to catch errors not at thread boundaries makes it impossible to safely export code through the C FFI without spawning a new thread. Rust started out with this restriction, whereby panics can only be caught by parent threads of a failing thread. The restriction was removed with the implementation of catch_unwind.

    Furthermore, carefully writing every data structure to implement strong exception safety is pointless when a compiler toggle can disable exception handling. Doubly so when writing a library, since control of whether or not to use exceptions falls on the client of that library (see below: Libraries Cannot Rely on Destructors).

12. Misuse of Exceptions: If catching an exception is possible, people will use it to implement a general try/catch mechanism, no matter how discouraged that is.

    For example, Rust’s catch_unwind is used in web servers. For example, in the docs.rs project, see here and here.

13. Minimum Common Denominator: Destructors are a minimum common denominator interface: a destructor is a function that takes an object and returns nothing, A -> ().

    Destructors force all resource-closing operations to conform to this interface, even if they can’t. The prototypical example has already been mentioned: fclose can return failure. How do languages with destructors deal with this?

    Again, in C++, closing a file object will explicitly forget that error, since throwing an exception would cause the program to abort. You are supposed to close the file manually, and protect that close function call from unwinding.

    Again, in Rust, closing a file will also ignore errors, because Rust works like C++ in that throwing from a destructor will abort the program. You can call sync_all before the destructor runs to ensure the buffer is flushed to disk. But, again: the compiler will not force you to call sync_all or to manually close the file.

    More generally, affine type systems cannot force the programmer to do anything: resources that are silently discarded will be destroyed by the compiler inserting a call to the destructor. Rust gets around this by implementing a cfg(must_use) annotation on functions, which essentially tells the compiler to force programmers to use the result code of that function.

14. Libraries Cannot Rely on Destructors: In C++, compilers often provide non-standard functionality to turn off exception handling. In this mode, throw is an abort and the body of a catch statement is dead code. Rust works similarly: a panic can cause stack unwinding (and concurrent destruction of stack objects) or a program abort, and this is configurable in the compiler. Unlike C++, this option is explicitly welcome in Rust.

    In both languages, the decision of whether or not to use exception handling takes place at the root of the dependency tree: at the application. This makes sense: the alternative is a model whereby a library that relies on unwinding will pass this requirement to other packages that depend on it, “infecting” dependents transitively up to the final application.

    For this reason, libraries written in either language cannot rely on unwinding for exception safety.

    It is not uncommon, however, for libraries to effectively rely on unwinding to occur in order to properly free resources. For example, the documentation for the easycurses library says:

    The library can only perform proper automatic cleanup if Rust is allowed to run the Drop implementation. This happens during normal usage, and during an unwinding panic, but if you ever abort the program (either because you compiled with panic=abort or because you panic during an unwind) you lose the cleanup safety. That is why this library specifies panic="unwind" for all build modes, and you should too.

    This is not a problem with the library, or with Rust. It’s just what it is.

15. Code in General Cannot Rely on Destructors: A double throw will abort, a stack overflow can abort, and a SIGABRT can abort the program, and, finally, the power cord can be pulled. In all of these cases, destructors will not be called.

    In the presence of exogeneous program termination, the only way to write completely safe code is to use side effects with atomic/transactional semantics.

Linear Types and Exceptions

Linear types are incompatible with exception handling. It’s easy to see why.

A linear type system guarantees all resources allocated by a terminating program will be freed, and none will be used after being freed. This guarantee is lost with the introduction of exceptions: we can throw an exception before the consumer of a linear resource is called, thus leaking the resource. In this section we go through different strategies for reconciling linear types and exceptions.

Motivating Example

If you’re convinced that linear types and exceptions don’t work together, skip this section. Otherwise, consider:

try {
  let f = open("/etc/config");
  // `write` consumes `f`, and returns a new linear file object
  let f' = write(f, "Hello, world!");
  throw Exception("Nope");
  close(f');
} catch Exception {
  puts("Leak!");
}

A linear type system will accept this program: f and f' are both used once. But this program has a resource leak: an exception is thrown before f' is consumed.

If variables defined in a try block can be used in the scope of the associated catch block, we could attempt a fix:

try {
  let f = open("/etc/config");
  let f' = write(f, "Hello, world!");
  throw Exception("Nope");
  close(f');
} catch Exception {
  close(f');
}

But the type system wouldn’t accept this: f' is potentially being consumed twice, if the exception is thrown from inside close.

Can we implement exception handling in a linearly-typed language in a way that preserves linearity guarantees? In the next three sections, we look at the possible approaches.

Solution A: Values, not Exceptions

We could try having exception handling only as syntactic sugar over returning values. Instead of implementing a complex exception handling scheme, all potentially-throwing operations return union types. This can be made less onerous through syntactic sugar. The function:

T nth(array<T> arr, size_t index) throws OutOfBounds {
  return arr[index];
}

Can be desugared to (in a vaguely Rust-ish syntax):

Result<T, OutOfBounds> nth(array<T> arr, size_t index) {
  case arr[index] {
    Some(elem: T) => {
      return Result::ok(elem);
    }
    None => {
      return Result::error(OutOfBounds());
    }
  }
}

This is appealing because much of the hassle of pattern matching Result types can be simplified by the compiler. But this approach is immensely limiting, because as stated above, many fundamental operations have failure modes that have to be handled explicitly:

add : (Int, Int) -> Result<Int, Overflow>
sub : (Int, Int) -> Result<Int, Overflow>
mul : (Int, Int) -> Result<Int, Overflow>
div : (Int, Int) -> Result<Int, Overflow | DivisionByZero>

nth : (Array<T>, Nat) -> Result<T, OutOfBounds>

As an example, consider a data structure implementation that uses arrays under the hood. The implementation has been thoroughly tested and you can easily convince yourself that it never accesses an array with an invalid index. But if the array indexing primitive returns an option type to indicate out-of-bounds access, the implementation has to handle this explicitly, and the option type will “leak” into client code, up an arbitrarily deep call stack.

The problem is that an ML-style type system considers all cases in a union type to be equiprobable, the normal path and the abnormal path have to be given equal consideration in the code. Exception handling systems let us conveniently differentiate between normal and abnormal cases.

Solution B: Use Integrated Theorem Provers

Instead of implementing exception handling for contract violations, we can use an integrated theorem prover and SMT solver to prove that integer division by zero, integer overflow, array index out of bounds errors, etc. never happen.

A full treatment of abstract interpretation is beyond the scope of this article. The usual tradeoff applies: the tractable static analysis methods prohibit many ordinary constructions, while the methods sophisticated enough to prove most code correct are extremely difficult to implement completely and correctly. Z3 is 300,000 lines of code.

Solution C: Capturing the Linear Environment

To our knowledge, this is the only sound approach to doing exception handling in a linearly-typed language that doesn’t involve fanciful constructs using delimited continuations.

PacLang is an imperative linearly-typed programming language specifically designed to write packet-processing algorithms for network procesors. The paper is worth reading.

Its authors describe the language as:

a simple, first order, call by value language, intended for constructing network packet processing programs. It resembles and behaves like C in most respects. The distinctive feature of PacLang is its type system, treating the datatypes that correspond to network packets within the program as linear types. The target platforms are application-specific network processor (NP) architectures such as the Intel IXP range and the IBM PowerNP.

The type system is straightforward: bool, int, and a linear packet type. A limited form of borrowing is supported, with the usual semantics:

In PacLang, the only linear reference is a packet. An alias to a reference of this type, a !packet, can be created in a limited scope, by casting a packet into a !packet if used as a function argument whose signature requires a !packet. An alias may never exist without an owning reference, and cannot be created from scratch. In the scope of that function, and other functions applied to the same !packet, the alias can behave as a normal non-linear value, but is not allowed to co-exist in the same scope as the owning reference packet. This is enforced with constraints in the type system:

• A !packet may not be returned from a function, as otherwise it would be possible for it to co-exist inscope with the owning packet

• A !packet may not be passed into a function as an argument where the owning packet is also being used as an argument, for the same reason

Any function taking a !packet cannot presume to “own” the value it aliases, so is not permitted to deallocate it or pass it to another a thread; this is enforced by the signatures of the relevant primitive functions. The constraints on the packet and !packet reference types combined with the primitives for inter-thread communication give a uniqueness guarantee that only one thread will ever have reference to a packet.

An interesting restriction is that much of the language has to be written in A-normal form to simplify type checking. This is sound: extending a linear type system to implement convenience features like borrowing is made simpler by working with variables rather than arbitrary expressions, and it’s a restriction Austral shares.

The original language has no exception handling system. PacLang++, a successor with exception handling support, is introduced in the paper Memory safety with exceptions and linear types. The paper is difficult to find, so I will quote from it often. The authors first describe their motivation in adding exception handling:

In our experience of practical PacLang programming, an issue commonly arising is that of functions returning error values. The usual solution has been to return an unused integer value (C libraries commonly use -1 for this practice) where the function returns an integer, or to add a boolean to the return tuple signalling the presence of an error or other unusual situation. This quickly becomes awkward and ugly, especially when the error condition needs to be passed up several levels in the call graph. Additionally, it is far easier for a programmer to unintentionally ignore errors using this method, resulting in less obvious errors later in the program, for example a programmer takes the return value as valid data, complacently ignoring the possibility of an error, and using that error value where valid data is expected later in the program.

The linear type system of PacLang:

A linearly typed reference (in PacLang this is known as the owning reference, though other kinds of non-linear packet references will be covered later) is one that can be used only once along each execution path, making subsequent uses a type error; the type system supports this by removing a reference (consuming it) from the environment after use. As copying a linear reference consumes it, only one reference (the owning reference) to the packet may exist at any point in the program’s runtime. Furthermore, a linear reference must be used once and only once, guaranteeing that any linearly referenced value in a type safe program that halts will be consumed eventually.

The authors first discuss the exceptions as values approach, discarding it because it doesn’t support intra-function exception handling, and requires all functions to deallocate live linear values before throwing. The second attempt is described by the authors:

At the time an exception is raised, any packets in scope must be consumed through being used as an argument to the exception constructor, being “carried” by the exception and coming into the scope of the block that catches the exception.

This is also rejected, because:

this method does not account for live packets that are not in scope at the time an exception is raised. An exception can pass arbitrarily far up the call graph through multiple scopes that may contain live packets until it is caught.

The third and final approach:

We create an enhanced version of the original PacLang type system, which brings linear references into the environment implicitly wherever an exception is caught. Our type system ensures that the environment starting a catch block will contain a set of references (that are in the scope of the exception handling block) to the exact same linear references that were live at the instant the exception was thrown.

To illustrate I adapted the following example from the paper, adding a few more comments:

packet x = recv();
packet y = recv();

// At this point, the environment is {x, y}

try {
  consume(x);
  // At this point, the environment is just {y}
  if (check(!y)) {
    consume(y);
    // Here, the environment is {}
  } else {
    throw Error; // Consumes y implicitly
    // Here, the environment is {}
  }
  // Both branches end with the same environment
} catch Error(packet y) {
  log_error();
  consume(y);
}

The authors go on to explain a limitation of this scheme: if two different throw sites have a different environment, the program won’t type check. For example:

packet x = recv();

// Environment is {x}
if (check(!x)) {
  packet y = recv();

  // Environment is {x, y}
  if (checkBoth(!x, !y)) {
    consume(x);
    consume(y);
    // Environment is {}
  } else {
    throw Error; // Consumes x and y
    // Environment is {}
  }
} else {
  throw Error; // Consumes x
  // Enviroment is {}
}

While the code is locally sound, one throw site captures x alone while one captures x and y.

Suppose the language we’re working with requires functions to be annotated with an exception signature, along the lines of [checked exceptions][checked]. Then, if all throw sites in a function f implicitly capture a single linear packet variable, we can annotate the function this way:

void f() throws Error(packet x)

But in the above code example, the exception annotation is ambiguous, because different throw sites capture different environments:

void f() throws Error(packet x)
// Or
void f() throws Error(packet x, packet y)

Choosing the former leaks y, and choosing the latter means the value of y will be undefined in some cases.

This can be fixed with the use of option types: because environments form a partially ordered set, we can use option types to represent bindings which are not available at every throw site. In the code example above, we have:

{} < {x} < {x, y}

So the signature for this function is simply:

void f() throws Error(packet x, option<packet> y)

In short: we can do it, but it really is just extra semantics and complexity for what is essentially using a Result type.

Affine Types and Exceptions

Affine types are a weakening of linear types, essentially linear types with implicit destructors. In a linear type system, values of a linear type must be used exactly once. In an affine type system, values of an affine type can be used at most once. If they are unused, the compiler automatically inserts a destructor call.

Rust does this, and there are good reasons to prefer affine types over linear types:

1. Less typing, since there is no need to explicitly call destructors.

2. Often, compilation fails because programmers make trivial mistakes, such as forgetting a semicolon. A similar mistake is forgetting to insert destructor calls. This isn’t possible with affine types, where the compiler handles object destruction for the programmer.

3. Destruction order is consistent and well-defined.

4. Most linear types have a single natural destructor function: pointers are deallocated, file handles are closed, database connections are closed, etc. Affine types formalize this practice: instead of having a constellation of ad-hoc destructor functions (deallocate, closeFile, closeDatabase, hangUp), all destructors are presented behind a uniform interface: a generic function of type T! -> Unit.

The drawbacks of affine types are the same as those of destructors in languages like C++ and Ada, that is:

1. The use of destructors requires compiler insertion of implicit function calls, which have an invisible cost in runtime and code size, whereas linear types make this cost visible.

2. Destruction order has to be well-specified. For stack-allocated variables, this is straghtforward: destructors are called in inverse declaration order. For temporaries, this is complicated.

Additionally, destroying values we don’t do anything with could lead to bugs if the programmer simply forgets about a value they were supposed to use, and instead of warning them, the compiler cleans it up.

But there is a benefit to using affine types with destructors: exception handling integrates perfectly well. Again, Rust does this: panic and catch_unwind are similar to try and catch, and destructors are called by unwinding the stack and calling drop on every affine object. The result is that exceptions are safe: in the happy path, destructors are called by the compiler. In the throwing path, the compiler ensures the destructors are called anyways.

The implementation strategy is simple:

1. When the compiler sees a throw expression, it emits calls to the destructor of every (live) affine variable in the environment before emitting the unwinding code.

   That is, given an expression throw(...), where the affine environment up to that expression is {x, y, z}, the expression is transformed into:

   free(x);
   free(y);
   free(z);
   throw(...);

2. When the compiler sees a call to a potentially-throwing function (as determined by an effect system), it emits a try/catch block: normal excecution proceeds normally, but if an exception is caught, the the destructors of all live affine variables are called, and the exception is re-thrown.

   Suppose we have a function call f(), where the affine environment up to the point of that call is {x, y}. If the function potentially throws an exception, the function call gets rewritten to something like this:

   let result = try {
     f();
   } catch Exception as e {
     free(x);
     free(y);
     throw(e);
   }

For a more complete example, a program like this:

void f() throws {
  let x: string* = allocate("A fresh affine variable");
  // Environment is {x}
  g(x); // Environment is {}
}

void g(string* ptr) throws {
  let y: string* = allocate("Another heap-allocated string");
  // Environment is {ptr, y}
  h(ptr); // Environment is {y}
}

void h(string* ptr) throws {
  let z = allocate(1234);
  if (randBool()) {
    throw "Halt";
  }
}

Would transform to something like this:

void f() {
  let x: string* = _allocate_str("A fresh affine variable");
  try {
    g(x);
  } catch {
    rethrow;
  }
}

void g(string* ptr) {
  let y: string* = _allocate_str("Another heap-allocated string");
  try {
    h(ptr);
  } catch {
    _free_str(y);
    rethrow;
  }
  _free_str(y);
}

void h(string* ptr) {
  let z = allocate(1234);
  if (randBool()) {
    _free_intptr(z);
    _free_str(ptr);
    throw "Halt";
  }
  _free_intptr(z);
  _free_str(ptr);
}

Prior Art

Herb Sutter, Zero-overhead deterministic exceptions: Throwing values:

An alternate result is never an “error” (it is success, so report it using return). This includes “partial suc- cess” such as that a buffer was too small for the entire request but was filled to capacity so more can be read on the next call.

[…]

A programming bug or abstract machine corruption is never an “error” (both are not programmatically re- coverable, so report them to a human, by default using fail-fast). Programming bugs (e.g., out-of-bounds ac- cess, null dereference) and abstract machine corruption (e.g., stack overflow) cause a corrupted state that can- not be recovered from programmatically, and so they should never be reported to the calling code as errors that code could somehow handle.

In the same vein, the Midori approach to exception handling:

A recoverable error is usually the result of programmatic data validation. Some code has examined the state of the world and deemed the situation unacceptable for progress. Maybe it’s some markup text being parsed, user input from a website, or a transient network connection failure. In these cases, programs are expected to recover. The developer who wrote this code must think about what to do in the event of failure because it will happen in well-constructed programs no matter what you do. The response might be to communicate the situation to an end-user, retry, or abandon the operation entirely, however it is a predictable and, frequently, planned situation, despite being called an “error.”

A bug is a kind of error the programmer didn’t expect. Inputs weren’t validated correctly, logic was written wrong, or any host of problems have arisen. Such problems often aren’t even detected promptly; it takes a while until “secondary effects” are observed indirectly, at which point significant damage to the program’s state might have occurred. Because the developer didn’t expect this to happen, all bets are off. All data structures reachable by this code are now suspect. And because these problems aren’t necessarily detected promptly, in fact, a whole lot more is suspect. Depending on the isolation guarantees of your language, perhaps the entire process is tainted.

In Swift, contract violations terminate the program. In Ada, contract violations will throw an exception. In Rust, contract violations can panic. Panic can unwind or abort, depending on a compiler switch. This is a pragmatic strategy: the application developer, rather than the library developer, chooses whether to unwind or abort.

In the specific case of overflow, Rust checks overflow on Debug builds, but uses two’s complement modular arithmetic semantics on Release builds for performance. This is questionable.

Conclusion

We started with the following error categories:

1. Physical Failure.

2. Abstract Machine Corruption.

3. Contract Violations.

4. Memory Allocation Failure.

5. Failure Conditions.

For points #1 and #2 we can do nothing. For points #4 and #5 we use values to represent failures. This leaves point #3, for which there are four error handling strategies:

1. Terminate the program.

2. Terminate the thread.

3. Linear type system with PacLang-like capturing of the linear environment.

4. Affine type system with stack unwinding and destructors.

We reject exception handling on the grounds of semantic complexity, implementational complexity, and unsolved fundamental issues like the double throw problem (refer to the 15 point list of problems with exception handling).

Without exception handling, there’s no benefit to an affine type system over a linear one. In fact, absent exception handling, affine types are strictly worse than linear types, because:

1. Values can be silently forgotted by mistake.

2. There are implicit function calls.

3. Destruction order can change without the code changing, thus making code more unpredictable.

The PacLang solution to integrating linear types and exceptions is essentially returning Result types, so it can be rejected on the grounds that it is too onerous.

That leaves us with two approaches:

1. On contract violation, terminate the program.

2. On contract violation, terminate the thread.

The choice between the two is essentially a choice between security and error reporting:

1. If we crash the program we can be more certain we’re being secure, but testing code that uses assertions becomes much harder: if we want to ensure a function crashes on a certain input, we have to spawn a whole new process to run that function and report back.

2. If we crash only the process, we can do better error reporting and make it cheaper to unit-test potentially crashing code. But it creates the potential for misuse: a programmer could spawn threads, have them crash, and continue running the program, accumulating leaked memory and hanging file handles. In a long-running server environment, this could lead to a DOS attack.

By a hair, we err on the side of correctness and prefer to terminate the program to assure security. Special compiler flags might exist for unit tests that change the behaviour from crashing the program to crashing the thread, so we can unit test crashing functions more cheaply.

Bibliography

1. Thrippleton, Richard, and Alan Mycroft. “Memory safety with exceptions and linear types.”

2. Tov, Jesse A., and Riccardo Pucella. “A theory of substructural types and control.” ACM SIGPLAN Notices. Vol. 46. No. 10. ACM, 2011.

Capability-Based Security

Seen from the surface, the Earth’s crust appears immense; seen from afar, it is the thinnest skin of silicon over a cannonball of iron many times its mass.

Analogously with software: we write masses of application code, but it sits on tens of millions of lines of open source code: the library ecosystem, both direct and transitive dependencies. This is far too much code for one team to audit. Avoiding dependencies in commercial software is unrealistic: you can’t write the universe from scratch, and if you do, you will lose out to competitors closer to the efficient frontier.

The problem is that code is overwhelmingly permissionless. Or, rather: all code has uniform root permissions. The size of today’s software ecosystems has introduced a new category of security vulnerability: the supply chain attack. An attacker adds malware to an innocent library used transitively by millions. It is downloaded and run, with the user’s permissions, on the computers of hundreds of thousands of programmers, and afterwards, on application servers.

The solution is capability-based security. Code shoud be permissioned. To access the console, or the filesystem, or the network, libraries should require the capability to do so. Then it is evident, from function signatures, what each library is able to do, and what level of auditing is required.

Furthermore: capabilities can be arbitrarily granular. Beneath the capability to access the entire filesystem, we can have a capability to access a specific directory and its contents, or just a specific file, further divided into read, write, and read-write permissions. For network access, we can have capabilities to access a specific host, or capabilities to read, write, and read-write to a socket.

Access to the computer clock, too, should be restricted, since accurate timing information can be used by malicious or compromised dependencies to carry out a timing attack or exploit a side-channel vulnerability such as Spectre.

Linear Capabilities

A capability is a value that represents an unforgeable proof of the authority to perform an action. They have the following properties:

1. Capabilities can be destroyed.

2. Capabilities can be surrended by passing them to others.

3. Capabilities cannot be duplicated.

4. Capabilities cannot be acquired out of thin air: they must be passed by the client.

Capabilities in Austral are implemented as linear types: they are destroyed by being consumed, they are surrended by simply passing the value to a function, they are non-duplicable since linear types cannot be duplicated. The fourth restriction must be implemented manually by the programmer.

Let’s consider some examples.

Example: File Access

Consider a non-capability-secure filesystem API:

module Files is
    -- File and directory paths.
    type Path: Linear;

    -- Creating and disposing of paths.
    function makePath(value: String): Path;
    function disposePath(path: Path): Unit;

    -- Reading and writing.
    generic [R: Region]
    function readFile(path: &[Path, R]): String;

    generic [R: Region]
    function writeFile(path: &![Path, R], content: String): Unit;
end module.

(Error handling etc. omitted for clarity.)

Here, any client can construct a path from a string, then read the file pointed to by that path or write to it. A compromised transitive dependency could then read the contents of /etc/passwd, or any file in the filesystem that the process has access to, like so:

let p: Path := makePath("/etc/passwd");
let secrets: String := readFile(&p);
-- Send this over the network, using an
-- equally capability-insecure network
-- API.

In the context of code running on a programmer’s development computer, that means personal information. In the context of code running on an application server, that means confidential business information.

What does a capability-secure filesystem API look like? Like this:

module Files is
    type Path: Linear;

    -- The filesystem access capability.
    type Filesystem: Linear;

    -- Given a filesystem access capability,
    -- get the root directory.
    generic [R: Region]
    function getRoot(fs: &[Filesystem, R]): Path;

    -- Given a directory path, append a directory or
    -- file name at the end.
    function append(path: Path, name: String): Path;

    -- Reading and writing.
    generic [R: Region]
    function readFile(path: &[Path, R]): String;

    generic [R: Region]
    function writeFile(path: &![Path, R], content: String): Unit;
end module.

This demonstrates the hieararchical nature of capabilities, and how granular we can go:

1. If you have a Filesystem capability, you can get the Path to the root directory. This is essentially read/write access to the entire filesystem.

2. If you have a Path to a directory, you can get a path to a subdirectory or a file, but you can’t go up from a directory to its parent.

3. If you have a Path to a file, you can read from it or write to it.

Each capability can only be created by providing proof of a higher-level, more powerful, broader capability.

Then, if you have a logging library that takes a Path to the logs directory, you know it has access to that directory and to that directory only. If a library doesn’t take a Filesystem capability, it has no access to the filesystem.

But: how do we create a Filesystem value? The next section explains this.

The Root Capability

Capabilities cannot be created out of thin air: they can only be created by proving proof that the client has access to a more powerful capability. This recursion has to end somewhere.

The root of the capability hierarchy is a value of type RootCapability. This is the first argument to the entrypoint function of an Austral program. For our capability-secure filesystem API, we’d add a couple of functions:

-- Acquire the filesystem capability, when the client can
-- provide proof that they have the root capability.
generic [R: Region]
function getFilesystem(root: &[RootCapability, R]): Filesystem;

-- Relinquish the filesystem capability.
function releaseFilesystem(fs: Filesystem): Unit;

And we can use it like so:

import Files (
    Filesystem,
    getFilesystem,
    releaseFilesystem,
    Path,
    getRoot,
    append,
);
import Dependency (
    doSomething
);

function main(root: Root_Capability): ExitCode is
    -- Acquire a filesystem capability.
    let fs: Filesystem := getFilesystem(&root);
    -- Get the root directory.
    let r: Path := getRoot(&fs);
    -- Get the path to the `/var` directory.
    let p: Path := Append(p, "var");
    -- Do something with the path to the `/var`
    -- directory, confident that nothing this
    -- dependency does can go outside `/var`.
    doSomething(p);
    -- Afterwards, relinquish the filesystem
    -- capability.
    releaseFilesystem(fs);
    -- Surrender the root capability. Beyond
    -- this point, the program can't do anything
    -- effectful.
    surrenderRoot(root);
    -- Finally, end the program by returning
    -- the success status code.
    return ExitSuccess();
end;

The FFI Boundary

Ultimately, all guarantees are lost at the FFI boundary. Because foreign functions are permissionless, we can implement both the capability-free and the capability-secure APIs in Austral. Does that mean these guarantees are worthless?

No. To use the FFI, a module has to be marked as unsafe using the Unsafe_Module pragma.

The idea is that a list of unsafe modules in all dependencies (including transitive ones) can be collected by the build system. Then, only code at the FFI boundary needs to be audited, to ensure that it correctly wraps the capability-insecure outside world under a correct, linear, capability-secure API.

Syntax

This section describes Austral’s syntax using EBNF.

(Note: the most up-to-date description of Austral’s syntax is the Menhir syntax definition here. This section is out of date.)

Meta-Language

Quick guide: definition is =, definitions are terminated with with ;. Concatenation is ,. Alternation is |. Optional is [...]. Repetition (zero or more) is {...}.

The syntax has two start symbols: one for interface files, and one for module body files.

Modules

module interface = [docstring], {import}, "interface", module name, "is"
                   {interface declaration}, "end.";

module body = [docstring], {import}, "module", module name, "is",
              {declaration}, "end.";

import = "import", module name, ["as", identifier], ["(", imported symbols, ")"], ";";

imported symbols = identifier, ",", imported symbols
                 | identifier;

interface declaration = constant declaration
                      | type declaration
                      | opaque type declaration
                      | function declaration


declaration = constant declaration
            | type declaration
            | function declaration

Declarations

constant declaration = "constant", identifier, ":", Type, ":=", expression;

type declaration = ;

opaque type declaration = "type", identifier, ";";

function declaration = ;

Identifiers

module name = module identifier, ".", module name
            | module identifier;

module identifier = identifier;

identifier = letter, {identifier character};
identifier character = letter | digit;

Comments and Documentation

comment = "-- ", {any character}, "\n";

docstring = "\"\"\"\n", { any character - "\"\"\"" } ,"\n\"\"\"";

Literals

digits = digit, { digit | "_" };
integer constant = ["+", "-"], digits;
float constant = digits, ".", digits, ["e", ["+", "-"], integer constant];
string constant = '"', { any character - '"' | '\"' }, '"';

Auxiliary Non-Terminals

Letter = uppercase | lowercase;
uppercase = "A" | "B" | "C" | "D" | "E" | "F" | "G" | "H" | "I" | "J"
          | "K" | "L" | "M" | "N" | "O" | "P" | "Q" | "R" | "S" | "T"
          | "U" | "V" | "W" | "X" | "Y" | "Z"
lowercase = "a" | "b" | "c" | "d" | "e" | "f" | "g" | "h" | "i" | "j"
          | "k" | "l" | "m" | "n" | "o" | "p" | "q" | "r" | "s" | "t"
          | "u" | "v" | "w" | "x" | "y" | "z"
digit = "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9";
symbol = "$" | "?" | "'"

Module System

Modules are the unit of code organization in Austral. Modules have two parts: the module interface file and the module body file.

Module Interfaces

The interface contains declarations that are importable by other modules.

A module interface can have the following declarations:

• Opaque constant declarations
• Record definitions
• Union definitions
• Function declarations
• Typeclass definitions
• Instance declarations

Module Bodies

The module body contains private declarations (that are not importable by other modules), as well as declarations that provide the definitions of opaque declarations in the module interface.

A module body can have the following kinds of declarations:

• Constant definitions
• Record definitions
• Union definitions
• Function definitions
• Typeclass definitions
• Instance definitions

Imports

Imports are the mechanism through which declarations from other modules are brought into an Austral module.

Imports appear at the top of both the module interface and module body files, before the module or module body keywords.

An import statement has the general form:

\[ \text{import} ~ m ~ ( \text{p}_1 ~ \text{as} ~ \text{l}_1, \dots, \text{n}_n ~ \text{as} ~ \text{l}_n ); \]

Where:

1. \(m\) is the name of the module to import the declarations from.
2. \(p\) is one of:
   1. The name of a declaration in \(m\).
   2. The name of a union case in a public union in \(m\).
   3. The name of a method in a public typeclass in \(m\).
3. \(l\) is the local nickname of \(p\): that is, appearances of \(l\) in the file where this import statement appears will be interpreted as though they were references to \(p\).

Note that import nicknames are not mandatory, and without them, the statement looks like:

\[ \text{import} ~ m ~ ( \text{p}_1, \dots, \text{p}_n ); \]

If an identifier \(p\) is imported without a nickname, references to \(p\) in the source text will be interpreted as references to that foreign declaration, union case, or method.

Import Nicknames

Import nicknames serve a dual purpose:

1. If two modules \(A\) and \(B\) define a declaration with the same name \(p\), we can import both of them by assigning one or both of them a nickname, like:

   \[ \begin{aligned} ~\text{import} ~ A ~ (\text{p} ~ \text{as} ~ \text{a});\\ ~\text{import} ~ B ~ (\text{p} ~ \text{as} ~ \text{b}); \end{aligned} \]

2. They allow us to use shorter names for longer identifiers where necessary.

Instance Imports

When importing from a module \(M\), all public typeclass instances in \(M\) are imported automatically.

Unsafe Modules

An unsafe module is a module that can access FFI features. Specifically, an unsafe module can:

• Import declarations from the Austral.Memory module.
• Use the External_Name pragma.

To specify that a module is unsafe, the Unsafe_Module pragma must be used in the module body. For example:

module body Example is
    pragma Unsafe_Module;

    -- Can import from `Austral.Memory`, etc.
end module body.

Examples

Given the following interface file:

module Example is
    -- The constant `c` is importable, but the interface
    -- doesn't know its value.
    constant c : Float32;

    -- Modules that import `R` can access the fields
    -- `x` and `y` directly, because it is a public record.
    record R: Free is
        x: Int32,
        y: Int32
    end;

    -- Modules can refer to the type T, but don't know
    -- how it's implemented, and therefore can't construct
    -- instances of it without going through the API.
    type T;

    -- Functions can only be declared, not defined, in
    -- interface files.
    function fact(n: Nat32): Nat32;

    -- Type classes must be defined with the full set of
    -- methods.
    typeclass Class(T: Type) is
        method foo(x: T): T;
    end;

    -- Instances are simply declared.
    instance Class(Int32);
end.

The following is a module definition that satisfies the interface:

module Example is
    constant c : Float32 := 3.14;

    -- Record `R` doesn't have to be redefined here,
    -- because it's already defined in the module interface.

    -- Type `T`, however, has to be defined. In this case
    -- it's a record.
    record T: Free is
        hidden: Bool;
    end;

    -- Function bodies must appear in the module body.
    function fact(n: Nat32): Nat32 is
        if n = 0 then
            return 1;
        else
            return n * fact(n-1);
        end if;
    end;

    -- Type class instances must be defined here:
    instance Class(Int32) is
        method foo(x: Int32): Int32 is
            return x;
        end;
    end;
end.

Type System

This section describes Austral’s type system.

Type Universes

Every concrete type belongs to a universe, which can be considered as the type of a type.

There are two universes:

1. The universe of unrestricted types, denoted Free. Bindings with a type in the Free universe can be used any number of times.
2. The universe of linear types, denoted Linear. These are explained in the next section.

Linear Types

A type \(\tau\) is linear if:

1. It contains another linear type. These types are called structurally linear.

2. Is it declared to be a linear type (see “Declaring Types”). These types are called declared linear.

To formalize the notion of “containment” in point 1.: a type \(\tau\) is said to contain a linear type \(\upsilon\) (or, equivalently, a type parameter \(\upsilon\) of kinds Linear or Type) if:

3. \(\tau\) is a record, where at least one field contains \(\upsilon\).
4. \(\tau\) is a union, where at least one case contains a field that contains \(\upsilon\).

Type Parameters

A type parameter has the form:

\[ \text{p}: K \]

where \(\text{p}\) is an identifier and \(K\) is a kind. The set of permitted kinds is:

• Free: a type parameter with kind Free accepts types that belong to the Free universe.

• Linear: a type parameter with kind Linear accepts types that belong to the Linear universe.

• Type: a type parameter with kind Type accepts any kind of type. Values with this type are treated as though they were Linear (i.e., they can only be used once, they can’t be silently dropped, etc.) since this is the lowest common denomination of behaviour.

• Region: a type parameter with kind Region accepts regions.

Type Parameter Constraints

Type parameters are “universally quantified”, meaning we can’t use any behaviour specific to the type. All we can do with an unknown type T is stuff it in a data structure or move it around. If we want to compare two instances of T for equality, for example, we’d have to pass a function pointer to a comparison function.

Type parameter constraints solve this, by allowing us to constrain a type parameter to only accept types that implement a set of typeclasses.

Let \(\text{p}\) be a type parameter name, \(\text{U}\) be one of \(\{Free, Linear, Type\}\), and \(\{C_1, ..., C_n\}\) be a set of type class names. Then:

\[ \text{p}: U(C_1, ..., C_n) \]

Denotes a type parameter constrained to only accept types that implement every listed class.

For example:

generic [T: Free(Printable, TotalEquality)]
function ...

Declaring Types

When declaring a type, we must state which universe it belongs to. This is so that the programmer is aware of type universes, and these are not relegated to just an implementation detail of the memory management scheme.

The rules around declaring types are:

1. A type that is not structurally linear can be declared to be Linear, and will be treated as an Linear type.
2. A type that is structurally linear cannot be declared as belonging to the Free universe.

In the case of generic types, we often want to postpone the decision of which universe the type belongs to. For example:

record Singleton[T: Type]: ??? is
    value: T
end;

Here, the type parameter T can accept types in both the Free and Linear universes. If we had to declare a universe for Singleton, the only way to make this type-check would be to declare that Singleton is in the Linear universe, since that is the lowest common denominator.

However, Austral lets us do this:

record Singleton[T: Type]: Type is
    value: T
end;

When Type appears as the declared universe of a type, it is not a universe, but rather, it tells the compiler to choose the universe when a concrete type is instantiated, using the algorithm described in “Automatic Universe Classification”. So Singleton[Int32] would be in the Free universe, but Singleton[U] (where U : Linear) belongs to the Linear universe.

Built-In Types

The following types are built into austral and available to all code.

Unit

type Unit: Free;

Unit is the type of functions that return no useful value. The only value of type Unit is the constant nil.

Boolean

type Bool: Free;

Bool is the type of logical and comparison operators.

The only Bool values are the constants true and false.

Integer Types

The following integer types are available:

All are in the free universe.

The Index type is the type of array indices.

Floating Point Types

type Float32: Free;
type Float64: Free;

The two floating-point types are Float32 and Float64.

Read-Only Reference

type Reference[T: Linear, R: Region]: Free;

The type Reference is the type of read-only references to linear values. Values of this type are bound to a region and are acquired by borrowing.

Syntactic sugar is available: &[T, R] expands to Reference[T, R].

Read-Write Reference

type WriteReference[T: Linear, R: Region]: Free;

The type WriteReference is the type of read-write references to linear values. Values of this type are bound to a region and are acquired by borrowing.

Syntactic sugar is available: &![T, R] expands to WriteReference[T, R].

Root Capability

type RootCapability: Linear;

The type RootCapability is the root of the capability hierarchy. It is the type of the first parameter to the entrypoint function.

Fixed-Size Arrays

type FixedArray[T: Free]: Free;

FixedArray is the type of arrays whose size is fixed, but not necessarily known at compile time. The type of string literals is FixedArray[Nat8].

Function Pointer Types

type Fn[A_0: Type, ..., A_n: Type, R: Type]: Free

Fn is the type of function pointers. It is always free.

Type Classes

Type classes, borrowed from Haskell 98, give us a bounded and sensible form of ad-hoc polymorphism.

Instance Uniqueness

In Austral, instances have to be globally unique: you can’t have multiple instances of the same typeclass for the same type, or for overlapping type parameters. So, the following are prohibited:

instance TC(Nat32);
instance TC(Nat32);

But also these:

generic [T: Type]
instance TC(Pointer[T]);

generic [T: Linear]
instance TC(Pointer[T]);

Enforcing uniqueness, however, does not require loading the entire program in memory. It only requires enforcing these three rules:

1. Within a module, no instances overlap.

2. You are only allowed to define instances for:

   1. Local typeclasses and local types.

   2. Local typeclasses and foreign types.

   3. Foreign typeclasses and local types.

   But you are not allowed to define an instance for a foreign typeclass and a foreign type.

Instance Resolution

This section describes how an instance is resolved from a method call.

Consider a typeclass:

typeclass Printable(T: Free) is
    method Print(t: T): Unit;
end;

And a set of instances:

instance Printable(Unit);
instance Printable(Bool);
generic [U: Type]
instance Printable(Pointer[U]);

Then, given a call like Print(true), we know Print is a method in the typeclass Printable. Then, we match the parameter list (t: T) to the argument list (true) and get a set of type parameter bindings { T => true }. The set will be the singleton set because typeclass definitions can only have one type parameter.

In this case, true is called the dispatch type.

Then we iterate over all the visible instances of the type class Printable (i.e.: those that are defined in or imported into the current module), and find the instance where the instance argument matches the dispatch type.

In the case of a concrete instance that’s just comparing the types for equality, and we’ll find the instance of Printable for Boolean.

Consider a call like Print(ptr) where ptr has type Pointer[Nat8]. Then, we repeat the process, except we’ll find a generic instance of Printable. Matching Pointer[U] to Pointer[Nat8] produces the bindings set { U => Nat8 }.

Declarations

This section describes the kind of declarations that can appear in Austral modules.

Opaque Constant

If c is an identifier, T is a type specifier, then:

constant c : T;

is an opaque constant declaration.

These can only appear in the module interface file, and must be accompanied by a matching constant declaration in the module body file.

Example:

module Example is
    -- Defines a public constant `Pi`, which can be imported
    -- and used by other modules.
    constant pi : Float64;
end module.

module body Example is
    -- An opaque constant declaration needs a matching constant
    -- definition in the module body.
    constant pi : Float64 := 3.14;
end module body.

Constant Definition

If c is an identifier, T is a type specifier, and E is a constant expression of type T, then:

constant c : T := V;

Defines a constant named C of type T with a value of V.

Constant definitions can only appear in the module body file.

If the module interface file has a corresponding opaque constant declaration, then the constant is public and can be imported by other modules. Otherwise, it is private.

Example:

module body Example is
    -- If there is no corresponding opaque constant declaration
    -- in the module interface file, then this constant is private
    -- and can't be used by other modules.
    constant Pi : DoubleFloat := 3.14;
end module body.

Record Definition

A record is an unordered collection of values, called fields, which are addressed by name.

If \(R\) is an identifier, \(\{R_0, ..., R_n\}\) is a set of identifiers, and \(\{T_0, ..., T_n\}\) is a set of type specifiers, then:

record R is
  R_0 : T_0;
  R_1 : T_1;
  ...
  R_n : T_n;
end

Defines the record R.

Unlike C, records in Austral are unordered, and the compiler is free to choose how the records will be ordered and laid out in memory. The compiler must select a single layout for every instance of a given record type.

Examples

Given the record:

record Vector3 is
    x : Float32;
    y : Float32;
    z : Float32;
end

We can construct an instance of Vector3 in two ways:

let V1 : Vector3 := Vector3(0.0, 0.0, 0.0);
let V2 : Vector3 := Vector3(
    x => 0.0,
    y => 0.0,
    z => 0.0
);

Union Definition

Unions are like datatypes in ML and Haskell. They have constructors and, optionally, constructors have values associated to them.

When a constructor has associated values, it’s either:

1. A single unnamed value.
2. A set of named values, as in a record.

For example, the definition of the Optional type is:

union Optional[T : Type] is
  case Some(T);
  case None;
end

union Color is
  case RGB(red: Nat8, green: Nat8, blue: Nat8);
  case Greyscale(Nat8);
end

Union creation:

let O2 : Optional[Int32] := None();
let O2 : Optional[Int32] := Some(10);
let C1 : Color := RGB(10, 12, 3);
let C2 : Color := RGB(
    red => 1,
    green => 2,
    blue => 3
);
let C3 : Color := Greyscale(50);

Function Declaration

Let \(\text{f}\) be an identifier, \(\{\text{p}_1: \tau_1, \dots, \text{p}_n: \tau_n\}\) be a set of value parameters, and \(\tau_r\) be a type. Then:

\[ \text{function} ~ \text{f} ( \text{p}_1: \tau_1, \dots, \text{p}_n: \tau_n ): \tau_r ; \]

declares a concrete function \(\text{f}\) with the given value parameter set and return type \(\tau_r\).

More generally, given a set of type parameter \(\{\text{tp}_1: k_1, \dots, \text{tp}_n: k_n\}\), then:

\[ \begin{aligned} & \text{generic} ~ [ \text{tp}_1: k_1, \dots, \text{tp}_n: k_n ] \\ & \text{function} ~ \text{f} ( \text{p}_1: \tau_1, \dots, \text{p}_n: \tau_n ): \tau_r ; \end{aligned} \]

declares a generic function \(\text{f}\) with the given type parameter set, value parameter set, and return type \(\tau_r\).

There must be a corresponding function definition in the module body file that has the same signature.

Function declarations can only appear in the module interface file.

Examples:

1. The following declares the identity function, a generic function with a single type parameter and a single value parameter:

   generic (t : Type)
   function Identity(x: T): T is
       return x;
   end

Function Definition

Let \(\text{f}\) be an identifier, \(\{\text{p}_1: \tau_1, \dots, \text{p}_n: \tau_n\}\) be a set of value parameters, \(\tau_r\) be a type, and \(s\) be a statement. Then:

\[ \begin{aligned} & \text{function} ~ \text{f} ( \text{p}_1: \tau_1, \dots, \text{p}_n: \tau_n ): \tau_r ~ \text{is} \\ & ~~~~ s \\ & \text{end} ; \end{aligned} \]

defines a concrete function \(\text{f}\) with the given value parameter set, return type \(\tau_r\), and body \(s\).

More generally, given a set of type parameter \(\{\text{tp}_1: k_1, \dots, \text{tp}_n: k_n\}\), then:

\[ \begin{aligned} & \text{generic} ~ [ \text{tp}_1: k_1, \dots, \text{tp}_n: k_n ] \\ & \text{function} ~ \text{f} ( \text{p}_1: \tau_1, \dots, \text{p}_n: \tau_n ): \tau_r ~ \text{is} \\ & ~~~~ s \\ & \text{end} ; \end{aligned} \]

defines a generic function \(\text{f}\) with the given type parameter set, value parameter set, return type \(\tau_r\), and body \(s\).

If there is a corresponding function declaration in the module interface file, the function is public, otherwise it is private.

Examples:

1. This defines a recursive function to compute the Fibonacci sequence:

   function fib(n: Nat64): Nat64 is
       if n <= 2 then
           return n;
       else
           return fib(n-1) + fib(n-2);
       end if;
   end

Typeclass Definition

Given:

1. Identifiers \(\text{t}\) and \(\text{p}\).

2. A universe \(u\).

3. A set of method signatures:

   \[ \left\{ \begin{aligned} & \text{m}\_1 ( \text{p}\_{11}: \tau\_{11}, \dots, \text{p}\_{1n}: \tau\_{1n} ): \tau\_1,\\ & \dots,\\ & \text{m}\_m ( \text{p}\_{m1}: \tau\_{m1}, \dots, \text{p}\_{mn}: \tau\_{mn} ): \tau\_m \end{aligned} \right\} \]

Then:

\[ \begin{aligned} & \text{typeclass} ~ \text{t} ( \text{p} : u ) ~ \text{is} \\ & ~~~~ \text{method} ~ \text{m}\_1 ( \text{p}\_{11}: \tau\_{11}, \dots, \text{p}\_{1n}: \tau\_{1n} ): \tau\_1 ; \\ & ~~~~ \dots; \\ & ~~~~ \text{method} ~ \text{m}\_m ( \text{p}\_{m1}: \tau\_{m1}, \dots, \text{p}\_{mn}: \tau\_{mn} ): \tau\_m ; \\ & \text{end} ; \end{aligned} \]

Defines a typeclass \(\text{t}\) with a parameter \(\text{p}\) which accepts types in the universe \(u\), and has methods \(\{\text{m}_1, ..., \text{m}_m\}\).

A typeclass declaration can appear in the module interface file (in which case it is public) or in the module body file (in which case it is private).

Examples:

1. Defines a typeclass Printable for types in the Type universe, with a method Print:

   typeclass Printable(T : Type) is
       method Print(value: T): Unit;
   end

Instance Declaration

Let \(\text{t}\) be the name of a typeclass and \(\tau\) be a type specifier. Then:

\[ \text{instance} ~ \text{t} ( \\tau ) ; \]

declares an instance of the typeclass \(\text{t}\) for the type \(\tau\).

Instance declaration can only appear in the module interface file, and must have a matching instance definition in the module body file.

An instance declaration means the instance is public.

Instance Definition

Given:

1. An identifier \(\text{t}\) that names name of a typeclass with universe \(u\).

2. A type specifier \(\tau\) in the universe \(u\).

3. A set of method definitions:

   \[ \left\{ \begin{aligned} &\text{m}\_1 ( \text{p}\_{11}: \tau\_{11}, \dots, \text{p}\_{1n}: \tau\_{1n} ): \tau\_1 ~ \text{is} ~ s_1,\\ &\dots,\\ &\text{m}\_m ( \text{p}\_{m1}: \tau\_{m1}, \dots, \text{p}\_{mn}: \tau\_{mn} ): \tau\_m ~ \text{is} ~ s_m \end{aligned} \right\} \]

Then:

\[ \begin{aligned} & \text{instance} ~ \text{t} ( \tau ) ~ \text{is} \\ & ~~~~ \text{method} ~ \text{m}\_1 ( \text{p}\_{11}: \tau\_{11}, \dots, \text{p}\_{1n}: \tau\_{1n} ): \tau\_1 ~ \text{is} ; \\ & ~~~~~~~~ s_1 ; \\ & ~~~~ \text{end} ; \\ & ~~~~ \dots; \\ & ~~~~ \text{method} ~ \text{m}\_m ( \text{p}\_{m1}: \tau\_{m1}, \dots, \text{p}\_{mn}: \tau\_{mn} ): \tau\_m ~ \text{is} ; \\ & ~~~~~~~~ s_m ; \\ & ~~~~ \text{end} ; \\ & \text{end} ; \end{aligned} \]

defines a concrete instance of the typeclass \(\text{t}\).

More generally, given a set of type parameters \(\{\text{tp}_1: k_1, \dots, \text{tp}_n: k_n\}\), then:

\[ \begin{aligned} & \text{generic} ~ [ \text{tp}_1: k_1, \dots, \text{tp}_n: k_n ] \\ & \text{instance} ~ \text{t} ( \tau ) ~ \text{is} \\ & ~~~~ \text{method} ~ \text{m}\_1 ( \text{p}\_{11}: \tau\_{11}, \dots, \text{p}\_{1n}: \tau\_{1n} ): \tau\_1 ~ \text{is} ; \\ & ~~~~~~~~ s_1 ; \\ & ~~~~ \text{end} ; \\ & ~~~~ \dots; \\ & ~~~~ \text{method} ~ \text{m}\_m ( \text{p}\_{m1}: \tau\_{m1}, \dots, \text{p}\_{mn}: \tau\_{mn} ): \tau\_m ~ \text{is} ; \\ & ~~~~~~~~ s_m ; \\ & ~~~~ \text{end} ; \\ & \text{end} ; \end{aligned} \]

defines a generic instance of the typeclass \(\text{t}\).

Examples:

typeclass Printable(T : Type) is
    method Print(value: T): Unit;
end

instance Printable(Int32) is
    method Print(value: Int32): Unit is
        printInt(value);
    end
end

Statements

This section describes the semantics of Austral statements.

Skip Statement

The skip statement is a no-op;

Example:

skip;

Let Statement

If N is an identifier, T is a type specifier, and E is an expression of type T, then:

let N: T := e;

is a let statement which defines a variable with name N, type T, and initial value E.

A let statement is one of the few places where type information flows forward: the declared type is used to disambiguate the type of the expression when the expression is, for example, a call to a return-type polymorphic function.

Let-destructure Statement

A let-destructure statement is used to break apart records, creating a binding for each field in the record.

The utility of this is: when you have a linear record type, you can’t extract the value of a linear field from it, because it consumes the record as a whole, and leaves unconsumed any other linear fields in the record. So the record must be broken up into its constituent values, and then optionally reassembled.

If R is an expression of type T, and T is a record type with field set {R_1: T_1, ..., R_n: T_n}, then:

let {R_1: T_1, ..., R_n: T_n} := R;

is a let-destructure statement.

Since there are likely to be collisions between record field names and existing variable names, let-destructure statements optionally support binding to a different name.

If R is an expression of type T, and T is a record type with field set {R_1: T_1, ..., R_n: T_n}, and N_i is an identifier, then:

let {..., R_i as N_i: T_i, ...} := R;

is a let-destructure statement with renaming. None, some, or all of the bindings may be renamed.

An example of a let-destructure statement with no renaming:

let { symbol: String, Z: Nat8, A: Nat8 } := isotope;

An example of a let-destructure statement with some bindings renamed:

let { symbol: String, Z as atomic_number: Nat8, A as mass_number: Nat8 } := isotope;

Assignment Statement

If P is an lvalue of type T and E is an expression of type T, then:

P := E;

is an assignment statement that stores the value of E in the location denoted by P.

[TODO: describe the semantics of lvalues]

If Statement

If {e_1, ..., e_n} is a set of expression of boolean type, and {b_1, ..., b_n, b_else} is a set of statements, then:

if e_1 then
    b_1;
else if e_2 then
    b_2;
...
else if e_n then
    b_n;
else
    b_else;
end if;

Is the general form of an if statement.

An example if statement with a single branch:

if test() then
    doSomething();
end if;

An example if statement with a true branch and a false branch:

if test() then
    doSomething();
else
    doSomethingElse();
end if;

An example if statement with three conditions and an else branch:

if a() then
    doA();
else if b() then
    doB();
else if c() then
    doB()
else
    doElse();
end if;

An example if statement with two conditions and no else branch:

if a() then
    doA();
else if b() then
    doB();
end if;

Case Statement

If E is an expression of a union type with cases {C_1, ..., C_n} and each case has slots C_i = {S_i1: T_i1, ..., S_in T_im}, and {B_1, ..., B_n} is a set of statements, then:

case E of
    when C_1(S_11: T_11, S_12: T_12, ..., S_1m: T_1m) do
        B_1;
    ...
    when C_n(S_n1: T_n1, S_n2: T_n2, ..., S_nm: T_nm) do
        B_n;
end case;

is a case statement.

Case statements are used to break apart unions. For each case in a union, there must be a corresponding when clause in the case statement. Analogously: for each slot in a union case, the corresponding when clause must have a binding for that slot.

An example of using the case statement on a union whose cases have no slots:

union Color: Free is
    case Red;
    case Green;
    case Blue;
end;

let C : Color := Red();
case C of
    when Red do
        ...;
    when Green do
        ...;
    when Blue do
        ...;
end case;

An example of using the Option type:

let o: Option[Int32] := Some(10);
case o of
    when Some(value: Integer_32) do
        -- Do something with `value`.
    when None do
        -- Handle the empty case.
end case;

An example of using the Either type:

let e: Either[Bool, Int32] := Right(right => 10);
case e of
    when Left(left: Bool) do
        -- Do something with `left`.
    when Right(right: Int32) do
        -- Do something with `right`.
end case;

Since there are likely to be collisions between union case slot names and existing variable names, case statements optionally support binding to a different name.

If E is an expression of a union type with cases {C_1, ..., C_n} and each case has slots C_i = {S_i1: T_i1, ..., S_in T_im}, and {B_1, ..., B_n} is a set of statements, and N_ij is an identifier, then:

case E of
    ...
    when C_i(..., S_ij as N_ij: T_ij, ...) do
        B_i;
    ...
end case;

is a case statement with renaming. None, some, or all of the bindings may be renamed.

An example of a case statement with a renamed binding:

case response of
    when Some(value as payload: String) do
        -- do something with the response payload
    when None do
        -- handle the failure case
end case;

While Loop

If e is an expression of type Bool and b is a statement, then:

while e do
    b;
end while;

is a while loop that iterates as long as e evaluates to true.

Examples:

-- An infinite loop
while true do
    doForever();
end while;

For Loop

If i is an identifier, s is an expression of type Nat64, f is an expression of type Nat64, and b is a statement, and s <= f, then:

for i from s to f do
    b;
end for;

is a for loop where b is executed once for each value of i in the interval [s, f].

Examples:

for i from 0 to n do
    doSomething(i);
end for;

Borrow Statement

If X is a variable of a linear type T, X' is an identifier, R is an identifier, and B is a statement, then:

borrow X as X' in R do
  B;
end;

Is a borrow statement that borrows the variable X as a reference X' with type &[T, R] in a new region named R.

The variable X' is usable only in B, dually, the variable X cannot be used in B, i.e. while it is borrowed.

The mutable form of the borrow statement is:

borrow! X as X' in R do
  B;
end;

The only difference is that the type of X' is &![R, T].

Discarding Statement

If e is an expression, then:

e;

Evaluates that expression and discards its value.

Note that discarding statements are illegal where e is of a linear type.

Return Statement

If e is an expression, then:

return e;

Returns from the function with the value e.

Note that return statements are illegal where there are unconsumed linear values.

Expressions

This section describes the semantics of Austral expressions.

Nil Constant

The expression:

nil

has type Unit.

Boolean Constant

The Boolean constants are the identifiers true and false.

Integer Constant

Integer constants have type Int32 by default, but to improve programmer ergonomics, the compiler will try to find a type for an integer constant that makes the surrounding context work. E.g., if x is of type Nat8, then an expression like x + 3 will work, and the 3 will be interpreted to have type Nat8.

Float Constant

Floating-point number constants have type Float64.

String Constant

String constants have type FixedArray[Nat8].

Variable Expression

An identifier that’s not the nil or boolean constants is a local variable or global constant, whose type is determined from the lexical environment.

Arithmetic Expression

If a and b are two expressions of the same integer or floating point type N, then:

a+b
a-b
a*b
a/b

are all expressions of type N.

In the case of division, two rules apply:

• If b is zero: the program aborts due to a division-by-zero error.
• If N is a signed integer type, and a is the minimum value that fits in that integer type, and b is -1: the program aborts due to a signed integer overflow error.

Function Call

If \(\text{f}\) is the name of a function with parameters \(\{\text{p}_1: \tau_1, \dots, \text{p}_n: \tau_n\}\) and return type \(\tau_r\), and we have a set of expressions \(\{e_1: \tau_1, \dots, e_n: \tau_n\}\), then:

\[ \text{f}(e_1, \dots, e_n) \]

and:

\[ \text{f}(\text{p}_1 \Rightarrow e_1, \dots, \text{p}_n \Rightarrow e_n) \]

are identical function call expression whose type is \(\tau_r\).

Method Call

Let \(\text{m}\) be the name of a method in a typeclass \(\text{t}\). After instance resolution the method has parameters \(\{\text{p}_1: \tau_1, \dots, \text{p}_n: \tau_n\}\) and return type \(\tau_r\). Given a set of expressions \(\{e_1: \tau_1, \dots, e_n: \tau_n\}\), then:

\[ \text{m}(e_1, \dots, e_n) \]

and:

\[ \text{m}(\text{p}_1 \Rightarrow e_1, \dots, \text{p}_n \Rightarrow e_n) \]

are identical method call expression whose type is \(\tau_r\).

Record Constructor

If \(\text{r}\) is the name of a record type with slots \(\{\text{s}_1: \tau_1, \dots, \text{s}_n: \tau_n\}\), and we have a set of expressions \(\{e_1: \tau_1, \dots, e_n: \tau_n\}\), then:

\[ \text{r}(\text{s}_1 \Rightarrow e_1, \dots, \text{s}_n \Rightarrow e_n) \]

is a record constructor expression which evaluates to an instance of \(\text{r}\) containing the given values.

Union Constructor

Let \(\text{u}\) be a union type, with a case named \(\text{c}\) with slots \(\{\text{s}_1: \tau_1, \dots, \text{s}_n: \tau_n\}\), and we have a set of expressions \(\{e_1: \tau_1, \dots, e_n: \tau_n\}\), then:

\[ \text{c}(\text{s}_1 \Rightarrow e_1, \dots, \text{s}_n \Rightarrow e_n) \]

is a union constructor expression which evaluates to an instance of \(\text{u}\) with case \(\text{c}\) and the given values.

As a shorthand, if the slot set has a single value, \(\{\text{s}: \tau\}\), and the set of expressions also has a single value \(\{e\}\), then a simplified form is possible:

\[ \text{c}(\text{s}) \]

is equivalent to:

\[ \text{c}(\text{s} \Rightarrow e) \]

Cast Expression

The cast expression has four uses:

1. Clarifying the type of integer and floating point constants.

2. Converting between different integer and floating point types (otherwise, you get a combinatorial explosion of typeclasses).

3. Converting write references to read references.

4. Clarifying the type of return type polymorphic functions.

If \(e\) is an expression and \(\tau\) is a type, then:

\[ e : \tau \]

is the expression that tries to cast \(e\) to \(\tau\), and it evaluates to a value of type \(\tau\).

Semantics:

1. If \(e\) is an integer constant that fits in \(\tau\) (e.g.: \(e\) can’t be a negative integer constant if \(\tau\) is Nat8) then \(e : \tau\) is valid.

2. If \(e\) is an integer or floating point type, and \(\tau\) is an integer or floating point type, then \(e : \tau\) is valid.

3. If \(e: \&![T, R]\) and \(\tau\) is \(\&[T, R]\), then \(e: \tau\) is valid and downgrades the write reference to a read reference.

4. If \(e\) is a call to a return type-polymorphic function or method, and \(\tau\) can clarify the return type of \(e\), then \(e : \tau\) is a valid expression.

Comparison Expression

If \(a\) and \(b\) are both expressions of the same comparable type, then:

\[ \begin{aligned} a &= b \\ a &\neq b \\ a &< b \\ a &\leq b \\ a &> b \\ a &\geq b \end{aligned} \]

are comparison expressions with type Bool.

The following types are comparable:

• Unit
• Bool
• Every natural number type.
• Every integer type.
• Every floating point type.
• Address and Pointer from Austral.Memory.
• Function pointer types.

Conjunction Expression

If a and b are Boolean-typed expressions, then a and b is the short-circuiting and operator and evaluates to a Boolean value.

Disjunction Expression

If a and b are Boolean-typed expressions, then a or b is the short-circuiting or operator, and evaluates to a Boolean value.

Negation Expression

If e is a Boolean-typed expression, then not e evaluates to the negation of the value of e, a Boolean value.

If Expression

If c is a Boolean-typed expression, and t and f are expressions of the same type T, then:

if c then t else f

is an if expression. c is evaluated first, if is true, t is evaluated and its value is returned. Otherwise, f is evaluated and its value is returend. The result has type T.

Path Expression

The syntax of a path is: an expression called the head followed by a non-empty list of path elements, each of which is one of:

1. A slot accessor of the form .s where s is the name of a record slot.
2. A pointer slot accessor of the form ->s where s is the name of a record slot.
3. An array indexing element of the form [i] where i is a value of type Index.

Path expressions are used for:

1. Accessing the contents of slots and arrays.

2. Transforming references to records and arrays into references to their contents.

Semantics:

1. All paths must end in a path in the Free universe. That is, if x[23]->y.z is a linear type, the compiler will complain.

2. A path that starts in a reference is a reference. For example, if x is of type &[T, R], then the path x->y->z (assuming z is a record slot with type U) is of type &[U, R].

Examples:

pos.x
star->pos.ra
stars[23]->distance

Dereference Expression

If e is a reference to a value of type T, then:

!e

is a dereferencing expression that evaluates to the referenced value of type T.

Borrow Expressions

If x is a variable of a linear type T, then:

&x

is an anonymous read-only borrow, and is an expression of type &[T, R], where R is a nameless region, and

&!x

is an anonymous read-write borrow, and is an expression of type &![T, R], where R is a nameless region.

Borrow expressions cannot escape the statement where they appear. That is, if we write:

let r: &[T, R] := &x;

This will be rejected by the compiler because the region name R is introduced nowhere.

sizeof Expression

If T is a type specifier, then:

sizeof(T)

is an expression of type Index that evaluates to the size of the type in bytes.

Linearity Checking

This section describes Austral’s linearity checking rules.

The rules for linear types:

1. A type is linear if it physically contains a linear type, or is declared to be linear (belongs to either the Linear or Type universes).

2. A variable x of a linear type must be used once and exactly once in the scope in which it is defined, where “used once” means:

   1. If the scope is a single block with no changes in control flow, a variable that appears once anywhere in the block is used once.

   2. If the scope includes an if statement, the variable must be used once in every branch or it must not appear in the statement.

   3. Analogously, if the scope includes a case statement, the variable must be used once in every when clause, or it must not appear in the statement.

   4. If the scope includes a loop, the variable may not appear in the loop body or the loop start/end/conditions (because it would be used once for each iteration). Linear variables can be defined inside loop bodies, however.

   5. A borrow statement does not count as using the variable.

   6. Neither does a path that ends in a free value (this is the one concession to programmer ergonomics).

3. When a variable is used, it is said to be consumed. Afterwards, it is said to be in the consumed state.

4. If a variable is never consumed, or is consumed more than once, the compiler signals an error.

5. Linear values which are not stored in variables cannot be discarded.

6. You cannot return from a function while there are any unconsumed linear values.

7. A borrowed variable cannot appear in the body of the statement that borrows it.

Built-In Modules

This section describes Austral’s built-in modules, those which are available everywhere.

Austral.Memory Module

The Austral.Memory module contains types and functions for manipulating pointers and memory.

Pointer Type

Declaration:

type Pointer[T: Type]: Free;

Description:

This is the type of nullable pointers.

nullPointer Function

generic [T: Type]
function nullPointer(): Pointer[T];

Description:

Returns the null pointer for a given type.

allocate Function

Declaration:

generic [T: Type]
function allocate(): Pointer[T];

Description:

Allocates enough memory to hold a single value of type T. Analogous to calloc with a count argument of 1.

allocateBuffer Function

Declaration:

generic [T: Type]
function allocateBuffer(count: Index): Pointer[T];

Description:

Allocates enough memory to hold count items of type T in a contiguous chunk of memory. Analogous to calloc.

count must be at least 1.

load Function

Declaration:

generic [T: Type]
function load(pointer: Pointer[T]): T;

Description:

Dereferences a pointer and returns its value.

store Function

Declaration:

generic [T: Type]
function store(pointer: Pointer[T], value: T): Unit;

Description:

Stores value at the location pointed to by pointer.

deallocate Function

Declaration:

generic [T: Type]
function deallocate(pointer: Pointer[T]): Unit;

Description:

Deallocates the given pointer.

loadRead Function

Declaration:

generic [T: Type, R: Region]
function loadRead(ref: &[Pointer[T], R]): Reference[T, R];

Description:

Takes a reference to a pointer, and turns it into a reference to the pointed-to value.

loadWrite Function

Declaration:

generic [T: Type, R: Region]
function loadWrite(ref: &![Pointer[T], R]): WriteReference[T, R];

Description:

Takes a write reference to a pointer, and turns it into a write reference to the pointed-to value.

resizeArray Function

Declaration:

generic [T: Type]
function resizeArray(array: Pointer[T], size: Index): Option[Pointer[T]];

Description:

Resizes the given array, returning Some with the new location if allocation succeeded, and None otherwise.

memmove Function

Declaration:

generic [T: Type, U: Type]
function memmove(source: Pointer[T], destination: Pointer[U], count: Index): Unit;

Description:

Moves the count bytes stored at source to destination.

memcpy Function

Declaration:

generic [T: Type, U: Type]
function memcpy(source: Pointer[T], destination: Pointer[U], count: Index): Unit;

Description:

Copies the count bytes stored at source to destination.

positiveOffset Function

Declaration:

generic [T: Type]
function positiveOffset(pointer: Pointer[T], offset: Index): Pointer[T];

Description:

Applies a positive offset to a pointer. Essentially this is:

\[ \text{pointer} + \text{sizeof}(\tau) \times \text{offset} \]

negativeOffset Function

Declaration:

generic [T: Type]
function negativeOffset(pointer: Pointer[T], offset: Index): Pointer[T];

Description:

Applies a negative offset to a pointer. Essentially this is:

\[ \text{pointer} - \text{sizeof}(\tau) \times \text{offset} \]

Austral.Pervasive Module

The Austral.Pervasive module exports declarations which are imported by every module.

Option Type

Definition:

union Option[T: Type]: Type is
    case None;
    case Some is
        value: T;
end;

Description:

The Option is used to represent values that might be empty, for example, the return type of a function that retrieves a value from a dictionary by key might return None if the key does not exist and Some otherwise.

Either Type

Definition:

union Either[L: Type, R: Type]: Type is
    case Left is
        left: L;
    case Right is
        right: R;
end;

Description:

The Either type is used to represent values which may have one of two distinct possibilities. For example, a function might return a value of type Either[Error, Result].

fixedArraySize Function

Declaration:

generic [T: Type]
function fixedArraySize(arr: FixedArray[T]): Nat64;

Description:

The fixedArraySize function returns the size of a fixed array.

abort Function

Declaration:

function abort(message: Fixed_Array[Nat8]): Unit;

Description:

The abort function prints the given message to standard error and aborts the program.

RootCapability Type

Declaration:

type RootCapability : Linear;

Description:

The RootCapability type is meant to be the root of the capability hierarchy.

The entrypoint function of an Austral program takes a single value of type RootCapability. This is the highest permission level, available only at the start of the program.

surrenderRoot Function

function surrenderRoot(cap: RootCapability): Unit;

The surrenderRoot function consumes the root capability. Beyond this point the program can’t do anything effectful, except through unsafe FFI interfaces.

ExitCode Type

union ExitCode: Free is
    case ExitSuccess;
    case ExitFailure;
end;

The ExitCode type is the return type of entrypoint functions.

Integer Bound Constants

Declarations:

constant maximum_nat8: Nat8;
constant maximum_nat16: Nat16;
constant maximum_nat32: Nat32;
constant maximum_nat64: Nat64;

constant minimum_int8: Int8;
constant maximum_int8: Int8;

constant minimum_int16: Int16;
constant maximum_int16: Int16;

constant minimum_int32: Int32;
constant maximum_int32: Int32;

constant minimum_int64: Int64;
constant maximum_int64: Int64;

Description:

These constants define the minimum and maximum values that can be stored in different integer types.

TrappingArithmetic Typeclass

Definition:

typeclass TrappingArithmetic(T: Type) is
    method trappingAdd(lhs: T, rhs: T): T;
    method trappingSubtract(lhs: T, rhs: T): T;
    method trappingMultiply(lhs: T, rhs: T): T;
    method trappingDivide(lhs: T, rhs: T): T;
end;

Description:

The TrappingArithmetic typeclass defines methods for performing arithmetic that aborts on overflow errors.

ModularArithmetic Typeclass

Definition:

typeclass ModularArithmetic(T: Type) is
    method modularAdd(lhs: T, rhs: T): T;
    method modularSubtract(lhs: T, rhs: T): T;
    method modularMultiply(lhs: T, rhs: T): T;
    method modularDivide(lhs: T, rhs: T): T;
end;

Description:

The ModularArithmetic typeclass defines methods for performing arithmetic that wraps around without abort on overflow errors.

Typeclass Instances

Declarations:

instance TrappingArithmetic(Nat8);
instance TrappingArithmetic(Int8);
instance TrappingArithmetic(Nat16);
instance TrappingArithmetic(Int16);
instance TrappingArithmetic(Nat32);
instance TrappingArithmetic(Int32);
instance TrappingArithmetic(Nat64);
instance TrappingArithmetic(Int64);
instance TrappingArithmetic(Double_Float);

instance ModularArithmetic(Nat8);
instance ModularArithmetic(Int8);
instance ModularArithmetic(Nat16);
instance ModularArithmetic(Int16);
instance ModularArithmetic(Nat32);
instance ModularArithmetic(Int32);
instance ModularArithmetic(Nat64);
instance ModularArithmetic(Int64);

Description:

These are the built-in instances of the TrappingArithmetic and ModularArithmetic typeclasses.

Foreign Interfaces

This section describes Austral’s support for communicating with the outside world.

The C Interface

This section decribes Austral’s support for calling C code.

Functions

To call a foreign function, we must declare it. The syntax is the same as that of ordinary functions, except in the body of the function definition.

For example, consider the C function:

double sum(double* array, size_t length);

The declaration of this function would look like:

function Sum(array: Pointer[Float64], length: Index): Float64;

Note that, as in regular functions, the declaration is only needed if the function is to be public in the module in which it is defined.

The definition would look like:

function Sum(array: Pointer[Float64], length: Index): Float64 is
    pragma Foreign_Import(External_Name => "sum");
end;

That is, instead of a statement, there is only a Foreign_Import pragma, which takes a named argument External_Name, which must be a string constant with the name of the function to import.

Naturally, the function’s parameter list and return type must match those of the foreign function. See the following section for how C types are mapped to Austral types.

Mapping Types

In the following table, the C type on the first column corresponds to the Austral type on the second column.

Only the types in the second column are permitted to appear in the parameter list and return type of a foreign function.

Style Guide

This section describes acceptable Austral code style.

Case Convention

The case conventions are:

1. Modules: Ada_Case.With.Dot.Separators. Examples:
   1. MyApp.Core.Storage.SQL_Storage
   2. MyLib.Parsers.CSV.CSV_Types
2. Constants: snake_case. Examples:
   1. minimum_nat8 2, pi
3. Types: PascalCase. Examples:
   1. Nat8
   2. RootCapability
   3. CsvReader
4. Functions and methods: camelCase. Examples:
   1. fib
   2. getByTitle
   3. parseHtmlString
5. Type classes: PascalCase: Examples:
   1. Printable
   2. TrappingArithmetic
6. Variables: snake_case. Examples:
   1. x
   2. leading_wavefront_velocity

Appendix A: GNU Free Documentation License

Version 1.3, 3 November 2008

Copyright (C) 2000, 2001, 2002, 2007, 2008 Free Software Foundation, Inc. https://fsf.org/

Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.

0. PREAMBLE

The purpose of this License is to make a manual, textbook, or other functional and useful document “free” in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.

This License is a kind of “copyleft”, which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.

We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.

1. APPLICABILITY AND DEFINITIONS

This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions stated herein. The “Document”, below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as “you”. You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.

A “Modified Version” of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.

A “Secondary Section” is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document’s overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.

The “Invariant Sections” are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.

The “Cover Texts” are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.

A “Transparent” copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not “Transparent” is called “Opaque”.

Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript or PDF produced by some word processors for output purposes only.

The “Title Page” means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, “Title Page” means the text near the most prominent appearance of the work’s title, preceding the beginning of the body of the text.

The “publisher” means any person or entity that distributes copies of the Document to the public.

A section “Entitled XYZ” means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as “Acknowledgements”, “Dedications”, “Endorsements”, or “History”.) To “Preserve the Title” of such a section when you modify the Document means that it remains a section “Entitled XYZ” according to this definition.

The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty Disclaimers may have is void and has no effect on the meaning of this License.

2. VERBATIM COPYING

You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.

You may also lend copies, under the same conditions stated above, and you may publicly display copies.

3. COPYING IN QUANTITY

If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document’s license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.

If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.

If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.

It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.

4. MODIFICATIONS

You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:

• A. Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.
• B. List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release you from this requirement.
• C. State on the Title page the name of the publisher of the Modified Version, as the publisher.
• D. Preserve all the copyright notices of the Document.
• E. Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
• F. Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
• G. Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document’s license notice.
• H. Include an unaltered copy of this License.
• I. Preserve the section Entitled “History”, Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled “History” in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
• J. Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the “History” section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
• K. For any section Entitled “Acknowledgements” or “Dedications”, Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
• L. Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
• M. Delete any section Entitled “Endorsements”. Such a section may not be included in the Modified Version.
• N. Do not retitle any existing section to be Entitled “Endorsements” or to conflict in title with any Invariant Section.
• O. Preserve any Warranty Disclaimers.

If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version’s license notice. These titles must be distinct from any other section titles.

You may add a section Entitled “Endorsements”, provided it contains nothing but endorsements of your Modified Version by various parties—for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.

You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.

The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.

5. COMBINING DOCUMENTS

You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.

The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.

In the combination, you must combine any sections Entitled “History” in the various original documents, forming one section Entitled “History”; likewise combine any sections Entitled “Acknowledgements”, and any sections Entitled “Dedications”. You must delete all sections Entitled “Endorsements”.

6. COLLECTIONS OF DOCUMENTS

You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.

You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.

7. AGGREGATION WITH INDEPENDENT WORKS

A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an “aggregate” if the copyright resulting from the compilation is not used to limit the legal rights of the compilation’s users beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.

If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document’s Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.

8. TRANSLATION

Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.

If a section in the Document is Entitled “Acknowledgements”, “Dedications”, or “History”, the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.

9. TERMINATION

You may not copy, modify, sublicense, or distribute the Document except as expressly provided under this License. Any attempt otherwise to copy, modify, sublicense, or distribute it is void, and will automatically terminate your rights under this License.

However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior to 60 days after the cessation.

Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your receipt of the notice.

Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, receipt of a copy of some or all of the same material does not give you any rights to use it.

10. FUTURE REVISIONS OF THIS LICENSE

The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See https://www.gnu.org/licenses/.

Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License “or any later version” applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation. If the Document specifies that a proxy can decide which future versions of this License can be used, that proxy’s public statement of acceptance of a version permanently authorizes you to choose that version for the Document.

11. RELICENSING

“Massive Multiauthor Collaboration Site” (or “MMC Site”) means any World Wide Web server that publishes copyrightable works and also provides prominent facilities for anybody to edit those works. A public wiki that anybody can edit is an example of such a server. A “Massive Multiauthor Collaboration” (or “MMC”) contained in the site means any set of copyrightable works thus published on the MMC site.

“CC-BY-SA” means the Creative Commons Attribution-Share Alike 3.0 license published by Creative Commons Corporation, a not-for-profit corporation with a principal place of business in San Francisco, California, as well as future copyleft versions of that license published by that same organization.

“Incorporate” means to publish or republish a Document, in whole or in part, as part of another Document.

An MMC is “eligible for relicensing” if it is licensed under this License, and if all works that were first published under this License somewhere other than this MMC, and subsequently incorporated in whole or in part into the MMC, (1) had no cover texts or invariant sections, and (2) were thus incorporated prior to November 1, 2008.

The operator of an MMC Site may republish an MMC contained in the site under CC-BY-SA on the same site at any time before August 1, 2009, provided the MMC is eligible for relicensing.

ADDENDUM: How to use this License for your documents

To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:

    Copyright (C)  YEAR  YOUR NAME.
    Permission is granted to copy, distribute and/or modify this document
    under the terms of the GNU Free Documentation License, Version 1.3
    or any later version published by the Free Software Foundation;
    with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.
    A copy of the license is included in the section entitled "GNU
    Free Documentation License".

If you have Invariant Sections, Front-Cover Texts and Back-Cover Texts, replace the “with … Texts.” line with this:

    with the Invariant Sections being LIST THEIR TITLES, with the
    Front-Cover Texts being LIST, and with the Back-Cover Texts being LIST.

If you have Invariant Sections without Cover Texts, or some other combination of the three, merge those two alternatives to suit the situation.

If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.